奇安信攻防社区-CorCTF 2024 Rev DigestMe

CorCTF 2024 Rev DigestMe

本题为一个CorCTF中的digestme题目的wp，这是一个自制的特殊VM逆向，整个逆向过程一波三折，最后还需要用到Cuda来完成最后的收尾，也还算有趣

题目的谜面如下

> FizzBuzz101 was innocently writing a new, top-secret compiler when his computer was Crowdstriked. Worse, the recovery key is behind a hasher that he wrote and compiled himself, and he can't remember how the bits work! Can you help him get his life's work back?

总的来说，题目**本质上是一个hash算法**（笔者做题的时候无视了这个提示，后面吃了大亏）。

把文件下载下来以后，粗略看一下，会发现题目是非常简单的C代码，但是如果尝试f5会发现提示函数过大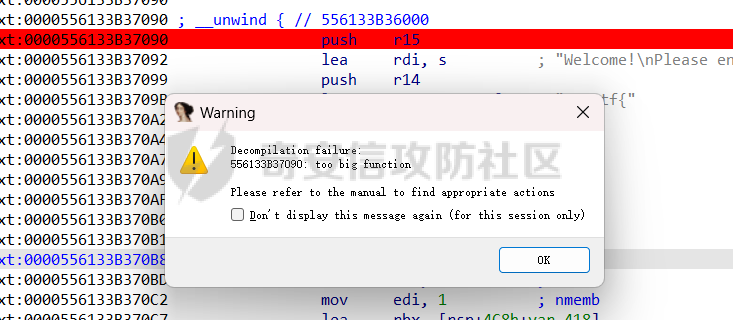

![func01.png](https://shs3.b.qianxin.com/attack_forum/2024/08/attach-d31e6bfc30ee3d3246af95de631db9c202767a43.png)

观察了一下，代码范围从`0x1090`到`0xED97F`，足足九十万行汇编。这么多的汇编，一看就没办法正常的进行分析了，这种题目就要开始学会取巧，使用各种各样的技巧尝试简化这个分析过程。

### 读题：简化逻辑

我们会发现，程序分成两部分，一部分是大量的重复操作：

```php
.text:0000000000001758                 mov     cl, [rax+0FA7h]
.text:000000000000175E                 or      cl, [rax+107h]
.text:0000000000001764                 mov     [rax+7], cl
.text:0000000000001767                 mov     cl, [rax+0FA8h]
.text:000000000000176D                 or      cl, [rax+108h]
.text:0000000000001773                 mov     [rax+8], cl
.text:0000000000001776                 mov     cl, [rax+0FA9h]
.text:000000000000177C                 or      cl, [rax+109h]
.text:0000000000001782                 mov     [rax+9], cl
.text:0000000000001785                 mov     cl, [rax+0FAAh]
.text:000000000000178B                 or      cl, [rax+10Ah]
.text:0000000000001791                 mov     [rax+0Ah], cl
```

另一部分是在程序开头比较普通的处理逻辑：

```php
.text:0000000000001090
.text:0000000000001090 ; __unwind {
.text:0000000000001090                 push    r15
.text:0000000000001092                 lea     rdi, s          ; "Welcome!\nPlease enter the flag here: "
.text:0000000000001099                 push    r14
.text:000000000000109B                 lea     r14, aCorctf    ; "corctf{"
.text:00000000000010A2                 push    r13
.text:00000000000010A4                 xor     r13d, r13d
.text:00000000000010A7                 push    r12
.text:00000000000010A9                 mov     r12d, 80000000h
.text:00000000000010AF                 push    rbp
.text:00000000000010B0                 push    rbx
.text:00000000000010B1                 sub     rsp, 498h
.text:00000000000010B8                 call    _puts
.text:00000000000010BD                 mov     esi, 186A0h     ; size
.text:00000000000010C2                 mov     edi, 1          ; nmemb
.text:00000000000010C7                 lea     rbx, [rsp+4C8h+var_418]
.text:00000000000010CF                 call    _calloc
.text:00000000000010D4                 lea     rbp, [rsp+4C8h+s]
.text:00000000000010DC                 mov     r15, rax
.text:00000000000010DF                 call    ___ctype_b_loc
.text:00000000000010E4                 mov     [rsp+4C8h+var_4C8], rax
.text:00000000000010E8                 lea     rax, [rsp+4C8h+s+8]
.text:00000000000010F0                 mov     [rsp+4C8h+var_4C0], rax
```

那么这里有一个技巧：可以试着将程序中间的某处patch 成`ret`，阻断ida对后续逻辑的分析，这样我们就能尝试用f5简单看看程序逻辑。当我们处理后，可以得到这样的逻辑:

```C
int main()
{
    char s[1000];
    char* v17 = &s[16];
    size_t v4; // rax
    puts("Welcome!\nPlease enter the flag here:");
    char* v3 = calloc(1, 0x186a0);
    // while ( 1 )
    // {
    memset(v17, 0, sizeof(v17));
    fgets(s, 999, stdin);
    v4 = strcspn(s, "\n");
     puts("Welcome!\nPlease enter the flag here: ");
  v3 = calloc(1uLL, 0x186A0uLL);
  v14 = __ctype_b_loc();
  while ( 1 )
  {
    memset(s, 0, sizeof(s));
    fgets(s, 999, stdin);
    v4 = strcspn(s, "\n");
    s[v4] = 0;
    if ( !memcmp("corctf{", s, 7uLL) && v4 > 1 && s[v4 - 1] == '}' && s[8] == s[17] && s[9] == s[11] )
    {
      v5 = s[7];
      if ( s[7] == s[16] + 1 && s[14] == s[16] + 4 )
      {
        v6 = &s[8];
        v7 = v3 + 0x940;
        v8 = *v14;
        if ( ((*v14)[s[7]] & 8) != 0 )
          break;
      }
    }
LABEL_14:
    puts("Try again: ");
  }
  while ( 1 )
  {
    v9 = v7;
    v10 = 7;
    do
    {
      v11 = v5 >> v10--;
      *v9 = v11;
      *v9++ &= 1u;
    }
    while ( v10 != -1 );
    v7 += 8;
    if ( &s[18] == v6 )
      break;
    v5 = *v6++;
    if ( (v8[(char)v5] & 8) == 0 )
      goto LABEL_14;
  }
  v3[2456] = 1;
  for ( i = 0LL; i != 64; ++i )
    v3[i + 2816] = ((0x8000000000000000LL >> i) & 0x5800000000000000LL) != 0;
  result = v3;
}

v3[319] = 1;
  v3[318] = 1;
  v3[317] = 1;
  v3[316] = 1;
  v3[315] = 1;
  v3[314] = 1;
  v3[313] = 1;
  v3[312] = 1;
  v3[311] = 1;
  v3[310] = 1;
  v3[309] = 1;
  v3[308] = 1;
  v3[307] = 1;
```

根据上述代码，首先可以总结出如下结论

- 初始化了一个巨大的内存空间，我们后文将会将其定义为`tmp`，在这里叫做`v3`
- 读入的字符串开头是`corctf{`，最后一个字符是`}`，这个题目中有直接体现

直接明文写在代码中，所以非常容易理解。然后，我们注意到有几个类似于字符串的约束关系

```C
s[8] == s[17]
s[9] == s[11]
s[7] == s[16] + 1
s[14] == s[16] + 4
```

而且我们会观察到，这个约束范围涉及的字符串从`s[7]~s[17]`，此时可以知道

- 输入**至少有18个字符是有效字符**

然后最后的循环中，我们还能看到一个循环边界

```cpp
if ( &s[18] == v6 )
    break;
```

这个v6来自于`&s[8]`，并且在循环中不断自增，其本质上为指向输入的指针，那么此时可以得出结论

- 读入的字符串长度大概率是19个字节，因为程序的循环有一处`&s[18]`用于描述循环的中断，这种中断大概率就是表示**字符串的处理结束**

此时我们就知道了flag的长度，然后接下来的逻辑就有一点匪夷所思，因为它不断地尝试的进行01的赋值

```cpp
 v3[317] = 1;
  v3[316] = 1;
  v3[315] = 1;
  v3[314] = 1;
  v3[313] = 1;
  v3[312] = 1;
  v3[311] = 1;
  v3[310] = 1;
```

并且下文中包含大量的重复加法或者异或操作

```cpp
  v3[4099] = 0;
  v3[4098] = 0;
  v3[4097] = 0;
  v3[4096] = 0;
  *v3 = v3[256] | v3[4000];
  v3[1] = v3[257] | v3[4001];
  v3[2] = v3[258] | v3[4002];
```

根据前文内容，`v3`整段内存都被提前初始化成了0，而且`v3[4000]`也是0，那么理论上这个`*v3 = v3[256] | v3[4000];`其实是无用的逻辑，这里笔者产生了一种想法

> 可能**可以利用gcc对一些无用逻辑进行优化**

具体做法就是：将当前反汇编的代码编写成有效的C代码，然后将当前的C代码进行编译，**使用gcc的规则替我们进行无用代码的删除**  
然而这个想法其实有缺陷的，毕竟我们没有办法将所有逻辑都罗列出来，所以gcc的优化存在一定的不足。最后优化的结果也是果然不太行，优化后的结果如下

```cpp
*((_QWORD *)v3 + 254) = 0x10100000000LL;
*((_QWORD *)v3 + 258) = 0x101010100010101LL;
v17 = 16777473;
*((_QWORD *)v3 + 260) = 0x100000001000101LL;
v3[1951] = 1;
*((_DWORD *)v3 + 486) = 0x10001;
*((_WORD *)v3 + 974) = 1;
v3[1950] = 1;
*((_QWORD *)v3 + 245) = 65537LL;
```

将一些01进行合并后，逻辑变得更加混乱，感觉并没有办法进行逻辑分析，只能放弃这种简化策略。

如果优化不管用，就意味着程序有另一种分析策略，就是汇编存在一定的规律，毕竟出题人不可能自己手搓超长汇编，这就意味着汇编的逻辑**存在某种循环**。我们这里展示一段汇编

```php
.text:0000000000001290                 mov     byte ptr [rax+13Fh], 1
.text:0000000000001297                 mov     byte ptr [rax+13Eh], 1
.text:000000000000129E                 mov     byte ptr [rax+13Dh], 1
.text:00000000000012A5                 mov     byte ptr [rax+13Ch], 1
.text:00000000000012AC                 mov     byte ptr [rax+13Bh], 1
.text:00000000000012B3                 mov     byte ptr [rax+13Ah], 1
.text:00000000000012BA                 mov     byte ptr [rax+139h], 1
.text:00000000000012C1                 mov     byte ptr [rax+138h], 1
.text:00000000000012C8                 mov     byte ptr [rax+137h], 1
.text:00000000000012CF                 mov     byte ptr [rax+136h], 1
.text:00000000000012D6                 mov     byte ptr [rax+135h], 1
.text:00000000000012DD                 mov     byte ptr [rax+134h], 1
.text:00000000000012E4                 mov     byte ptr [rax+133h], 1
.text:00000000000012EB                 mov     byte ptr [rax+132h], 1
.text:00000000000012F2                 mov     byte ptr [rax+131h], 1
.text:00000000000012F9                 mov     byte ptr [rax+130h], 1
.text:0000000000001300                 mov     byte ptr [rax+12Fh], 1
.text:0000000000001307                 mov     byte ptr [rax+12Eh], 1
.text:000000000000130E                 mov     byte ptr [rax+12Dh], 1
.text:0000000000001315                 mov     byte ptr [rax+12Ch], 1
.text:000000000000131C                 mov     byte ptr [rax+12Bh], 1
.text:0000000000001323                 mov     byte ptr [rax+12Ah], 1
.text:000000000000132A                 mov     byte ptr [rax+129h], 1
.text:0000000000001331                 mov     byte ptr [rax+128h], 1
.text:0000000000001338                 mov     byte ptr [rax+127h], 1
.text:000000000000133F                 mov     byte ptr [rax+126h], 1
.text:0000000000001346                 mov     byte ptr [rax+125h], 1
.text:000000000000134D                 mov     byte ptr [rax+124h], 1
.text:0000000000001354                 mov     byte ptr [rax+123h], 1
.text:000000000000135B                 mov     byte ptr [rax+122h], 1
.text:0000000000001362                 mov     byte ptr [rax+121h], 1
.text:0000000000001369                 mov     byte ptr [rax+120h], 1
.text:0000000000001370                 mov     byte ptr [rax+0FBFh], 0
```

仔细观察，会发现一个规律：这个赋值的过程中，`rax+13F`到`rax+120`之间，**正好进行了32个0的赋值**。而我们观察后文后，发现**至少也是按照8字节进行操作的循环**，所以我们可以得出两种结论：

- 程序可能是以8 bit（一字节）为操作最小单元
- 程序可能是以32 bit（四字节）为操作最小单元

进一步读汇编后，会发现汇编存在三种类型

- 将两个32字节连续的内存空间进行或处理
- 将两个32字节连续的内存空间进行与处理
- 将两个32字节连续的内存空间进行异或处理
- 将两个32字节连续的内存空间进行或/与/异或处理，同时混入`0B40h`和`0B41h`进行操作

前几种可以理解，应该是对两段内存空间进行与/或/异或处理，最后一个是什么逻辑呢？我们取出一小段分析

```php
.text:0000000000005DE9                 mov     [rax+9Fh], cl
.text:0000000000005DEF                 mov     cl, [rax+87h]
.text:0000000000005DF5                 xor     cl, [rax+7]
.text:0000000000005DF8                 mov     [rax+0A7h], cl
.text:0000000000005DFE                 mov     cl, [rax+87h]
.text:0000000000005E04                 and     cl, [rax+7]
.text:0000000000005E07                 mov     [rax+0B40h], cl
.text:0000000000005E0D                 mov     cl, [rax+86h]
.text:0000000000005E13                 xor     cl, [rax+6]
.text:0000000000005E16                 mov     [rax+0B41h], cl
.text:0000000000005E1C                 mov     cl, [rax+0B41h]
.text:0000000000005E22                 xor     cl, [rax+0B40h]
.text:0000000000005E28                 mov     [rax+0A6h], cl
```

如果我们将上述的操作写作代码理解，就是

```php
a[af] = a[87]^a[7]
a[B40] = a[87]&a[7]
a[b41] = a[86]^a[6]
a[ae] = a[b40]^a[b41]
```

如果这个时候正好学过机组，可能已经反应过来了，没有反应过来的也可以总结规律找到这个含义

- `a[af]=a[87]^a[7]`，意味着**只要两个操作数有一个为1，这个值就为1，否则这个值为0**
- `a[ae]=(a[87]&a[7])^(a[86]^a[6])`，这意味着**之前两个数均为1的时候，他们的结果将会影响下一个值得判断**

我们可以这样列一个表格来辅助我们思考

| `a[87]` | `a[7]` | `a[87]&a[7]` | `a[87]^a[7]` |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |

其中，`a[87]&a[7]`会影响**相邻得运算结果**，联系这个条件和表格，会发现这个表达式正是和**加法表达式**一摸一样，`a[87]&a[7]`象征着进位位，同时`a[87]^a[7]`象征着当前得数据。至此，我们可以总结出四种模拟得算法

- 与操作
- 或操作
- 加法操作
- 异或操作

并且分析加法操作得时候，我们可以通过观察内存排序，得到如下得规律

```php
           单个数据排列为小端序
0x1000000  [0 0 0 0 1 0 0 1]  [1 0 0 0 1 0 1 0]
              a[0] = 0x9            a[1] = 0x8a
0x1000008  [0 0 0 0 1 0 0 0]  [1 0 0 0 1 0 0 0]
              a[2] = 0x8            a[3] = 0x88

a = 0x88088a09
```

- 01串按照小端序
- 4个数字也按照小端序排序

根据这些规律，我们可以大胆猜测：程序就是用四字节进行操作基础，其中数据为小端序。此时，我们根据前面总结的所有规律，可以写出idapython脚本，将上述逻辑进行dump

```python

# mov byte [rsp-0xffset], value
def get_num(start_addr,idx):
    now_addr = start_addr
    value = 0
    for j in range(4):
        tmp_value = 0
        for i in range(8):
            v = idc.get_operand_value(now_addr, 1)
            tmp_value = tmp_value | (v<<i)
            now_addr = idc.next_head(now_addr)
        # print(hex(tmp_value))
        # value = (tmp_value<<(8*j)) + value
        value = (value << 8)+tmp_value

print("tmp[%d]=0x%x"%(idx, value))
    return value,now_addr

# tmp74 75 76 is our input
# tmp[88]=26
# tmp[89]=0
idaapi.process_ui_action("msglist:Clear")
start_addr = 0x1290
# end_addr = start_addr +0x10000
end_addr = 0xED854
# end_addr = 0x01F48 
now_addr = start_addr
index = 0
stack = [0] * 0x10000
while now_addr < end_addr:
    op = idc.print_insn_mnem(now_addr)
    if op == "mov":
        # consider mov operation
        op_type = idc.get_operand_type(now_addr, 1)
        # instant value
        # mov     byte ptr [rax+13Fh], 1
        if op_type == 5 and idc.get_operand_type(now_addr, 0) == 4:
            # load offset
            print("# mov addr:"+hex(now_addr))
            offset = idc.get_operand_value(now_addr, 0)
            # 8 times
            value,now_addr = get_num(now_addr, offset // 32)
            # set value to tmp stack
            stack[offset // 32] = value
            continue
        # operation start
        #  mov     cl, [rax+0FA0h]
        if op_type == 4 and idc.get_operand_type(now_addr, 0) == 1:
            # check next if or operation
            # print("check here:now_addr:"+hex(now_addr))
            n1 = idc.next_head(now_addr)
            n2 = idc.next_head(n1)
            if idc.print_insn_mnem(n1) == "or" and idc.get_operand_type(n1, 0) == 1 and idc.get_operand_type(n1, 1) == 4 and idc.print_insn_mnem(n2) == "mov" and  idc.get_operand_type(n2, 1) == 1:
                # or opreation
                # or / ror!
                # operation 32 dword
                print("# or addr:"+hex(now_addr))
                r_offset = idc.get_operand_value(n2, 0)
                op1_off = idc.get_operand_value(now_addr, 1)
                op2_off = idc.get_operand_value(n1, 1)
                if op1_off % 32 == r_offset % 32:
                    stack[r_offset//32] = stack[op1_off//32] | stack[op2_off//32]
                    print("tmp[%d]=tmp[%d]|tmp[%d]"%(r_offset//32,op1_off//32,op2_off//32))
                    for i in range(8*3*4):
                        now_addr = idc.next_head(now_addr)
                # print("after or now addr is " + hex(now_addr))
                else:
                    # or and ror
                    # print("# ror addr:"+hex(now_addr))
                    r_offset = idc.get_operand_value(n2, 0)
                    op1_off = idc.get_operand_value(now_addr, 1)
                    op2_off = idc.get_operand_value(n1, 1)

mov1_off = op1_off % 32
                    mov2_off = op2_off % 32

if mov1_off != mov2_off:
                        print("find abnormal sth")
                        exit()
                    else:
                        real_mov1_off = reverse_origin_offset(mov1_off)
                        real_target_off = reverse_origin_offset(r_offset%32)
                        stack[r_offset//32] = stack[op1_off//32] | stack[op2_off//32]
                        stack[r_offset//32] = rotate_right(stack[r_offset//32],(real_mov1_off-real_target_off)%32)
                        print("tmp[%d]=rotate_right(tmp[%d]|tmp[%d],%d)"%(r_offset//32,op1_off//32,op2_off//32,(real_mov1_off-real_target_off)%32))
                        for i in range(8*3*4):
                            now_addr = idc.next_head(now_addr)
                continue

if idc.print_insn_mnem(n1) == "and" and idc.get_operand_type(n1, 0) == 1 and idc.get_operand_type(n1, 1) == 4 and idc.print_insn_mnem(n2) == "mov" and  idc.get_operand_type(n2, 1) == 1:
                # and opreation
                print("# and addr:"+hex(now_addr))
                r_offset = idc.get_operand_value(n2, 0)
                op1_off = idc.get_operand_value(now_addr, 1)
                op2_off = idc.get_operand_value(n1, 1)
                stack[r_offset//32] = stack[op1_off//32] & stack[op2_off//32]
                print("tmp[%d]=tmp[%d]&tmp[%d]"%(r_offset//32,op1_off//32,op2_off//32))
                for i in range(8*3*4):
                    now_addr = idc.next_head(now_addr)
                continue
            if idc.print_insn_mnem(n1) == "xor" and idc.get_operand_type(n1, 0) == 1 and idc.get_operand_type(n1, 1) == 4 and idc.print_insn_mnem(n2) == "mov" and  idc.get_operand_type(n2, 1) == 1:
                # xor opreation
                # print("find xor")
                print("# xor addr:"+hex(now_addr))
                r_offset = idc.get_operand_value(n2, 0)
                op1_off = idc.get_operand_value(now_addr, 1)
                op2_off = idc.get_operand_value(n1, 1)
                stack[r_offset//32] =  stack[op1_off//32] ^ stack[op2_off//32]
                print("tmp[%d]=tmp[%d]^tmp[%d]"%(r_offset//32,op1_off//32,op2_off//32))
                for i in range(8*3*4):
                    now_addr = idc.next_head(now_addr)
                continue
            print("find new addr " +hex(now_addr))

else:
        print("new operation " + hex(now_addr))

now_addr = idc.next_head(now_addr)
```

能够得到初步得分析逻辑。

### 第一次解题挑战：Z3

乍一看逻辑，会发现逻辑种包含大量的普通的初始化操作

```php
tmp[9]=0xffffffff
tmp[125]=0x0
tmp[126]=0x0
tmp[127]=0x0
tmp[128]=0x0
tmp[0]=tmp[125]|tmp[8]
tmp[1]=tmp[126]|tmp[8]
tmp[2]=tmp[127]|tmp[8]
tmp[3]=tmp[128]|tmp[8]
tmp[10]=0xd76aa478
```

并且在后文还有各种运算操作

```php
mp[4]=tmp[5]|tmp[7]
tmp[5]=(tmp[4]+tmp[0])%0x100000000
tmp[6]=(tmp[5]+tmp[76])%0x100000000
tmp[4]=(tmp[6]+tmp[12])%0x100000000
tmp[0]=tmp[3]|tmp[8]
```

并且程序最后存在一个对数据恢复和比较的汇编逻辑

```php
.text:00000000000ED858                 mov     rsi, r15
.text:00000000000ED85B                 xor     edx, edx
.text:00000000000ED85D                 xor     edi, edi
.text:00000000000ED85F                 movups  [rsp+4C8h+var_4A8], xmm0
.text:00000000000ED864
.text:00000000000ED864 loc_ED864:                              ; CODE XREF: main+EC81C↓j
.text:00000000000ED864                 mov     r9d, edi
.text:00000000000ED867                 xor     ecx, ecx
.text:00000000000ED869                 sar     r9d, 5
.text:00000000000ED86D                 nop     dword ptr [rax]
.text:00000000000ED870
.text:00000000000ED870 loc_ED870:                              ; CODE XREF: main+EC7F8↓j
.text:00000000000ED870                 movsx   eax, byte ptr [rsi+rcx]
.text:00000000000ED874                 mov     r8d, r12d
.text:00000000000ED877                 shr     r8d, cl
.text:00000000000ED87A                 add     rcx, 1
.text:00000000000ED87E                 imul    eax, r8d
.text:00000000000ED882                 or      edx, eax
.text:00000000000ED884                 cmp     rcx, 20h ; ' '
.text:00000000000ED888                 jnz     short loc_ED870
.text:00000000000ED88A                 movsxd  r9, r9d
.text:00000000000ED88D                 add     edi, 20h ; ' '
.text:00000000000ED890                 add     rsi, 20h ; ' '
.text:00000000000ED894                 mov     dword ptr [rsp+r9*4+4C8h+var_4A8], edx
.text:00000000000ED899                 cmp     edi, 80h
.text:00000000000ED89F                 jz      short loc_ED8AE
.text:00000000000ED8A1                 mov     eax, edi
.text:00000000000ED8A3                 sar     eax, 5
.text:00000000000ED8A6                 cdqe
.text:00000000000ED8A8                 mov     edx, dword ptr [rsp+rax*4+4C8h+var_4A8]
.text:00000000000ED8AC                 jmp     short loc_ED864
.text:00000000000ED8AE ; ---------------------------------------------------------------------------
.text:00000000000ED8AE
.text:00000000000ED8AE loc_ED8AE:                              ; CODE XREF: main+EC80F↑j
.text:00000000000ED8AE                 cmp     dword ptr [rsp+4C8h+var_4A8+8], 19C603BAh
.text:00000000000ED8B6                 jnz     loc_1240
.text:00000000000ED8BC                 cmp     dword ptr [rsp+4C8h+var_4A8+0Ch], 14353CE4h
.text:00000000000ED8C4                 jnz     loc_1240
```

*注意，这里恢复的时候01按照小端序，字节按照大端序进行恢复*  
此时`rsi`和`r15`一样，指向我们之前操作的那些内存地址。那么本质上这里就是将内存地址的前16个字节读出来，假定为`tmp[0~3]`，我们就能够获得当前运算的最终结果判断逻辑：

- `tmp[2] == 0xba03c619`
- `tmp[3] == 0xe43c3514`

从逻辑上讲，我们现在有一些比较普通的与或运算，以及一个需要到达的答案数据，那么对于这类操作，大概率可以使用z3来进行解题。这里要简单提一嘴，虽然z3可以用使用`BitVec`进行异或位移的运算，但是大部分题目中都是以**无符号**的特性在使用他，所以我们在编写z3的时候也要尝试保持数据的无符号特性。

```python
from z3 import *

DEBUG = False
DEBUG = True

flag = [BitVec('bit%d' % i,8) for i in range(19)]
solver = Solver()

for i in range(len(flag)):
    solver.add(Or(And(ord('a') <= flag[i], flag[i] <= ord('z')),And(ord('0') <= flag[i], flag[i] <= ord('9')), And(ord('A') <= flag[i], flag[i] <= ord('Z'))))

solver.add(flag[0] == ord('c'))
solver.add(flag[1] == ord('o'))
solver.add(flag[2] == ord('r'))
solver.add(flag[3] == ord('c'))
solver.add(flag[4] == ord('t'))
solver.add(flag[5] == ord('f'))
# solver.add(flag[6] == ord('{'))
# solver.add(flag[-1] == ord("}"))

solver.add(flag[8] == flag[0x11])
solver.add(flag[9] == flag[0xb])
solver.add(flag[7] == (flag[0x10]+1))
solver.add((flag[0x10]+4) == flag[0xe])

tmp[74] = Concat(flag[10], flag[9], flag[8], flag[7])
tmp[75] = Concat(flag[14], flag[13], flag[12], flag[11])
tmp[76] = Concat(BitVecVal(0, 8), flag[17], flag[16], flag[15])
# tmp[76] += (0x80<<24)

print(tmp[74])
print(tmp[76])
# solver.add(tmp[74]+tmp[76] == 1)
# tmp[88]=0x58
# tmp[89]=0

# mov addr:0x1290
tmp[9]=0xffffffff
tmp[125]=0x0
tmp[126]=0x0
tmp[127]=0x0
tmp[128]=0x0
tmp[0]=tmp[125]|tmp[8]
# skip code
solver.add(tmp[2] == 0xba03c619)
solver.add(tmp[3] == 0xe43c3514)
if DEBUG:
    print("final tmp[2] = 0x%x"%tmp[2])
    print("final tmp[3] = 0x%x"%tmp[3])

if solver.check() == sat:
    m = solver.model()
    print(m)
    s = []
    for i in range(len(flag)):

print(chr(m[flag[i]].as_long()),end='')
```

然而，z3很快就提示找不到结果，这就说明约束出现了问题，有些地方一下子就被意识到出错了。重新分析初始化逻辑，会发现一段遗漏的逻辑

```c
  v3[2456] = 1;
  for ( i = 0LL; i != 64; ++i )
    v3[i + 2816] = ((0x8000000000000000LL >> i) & 0x5800000000000000LL) != 0;
  result = v3;
```

当初不理解的逻辑，在我们**理解它是32bit字节整数**这一点后，马上就能意识到，他初始化了两个内存地址

- `v3[0x998] = 1`相当于某一个32bit的数字的最高字节被初始化，加上前文提到的，输入长度为11字节，不难想到，为了保证运算的对齐，这里将最高位的数字初始化成了0x80
- `v3[b00~b20]` 被初始化,也就是`tmp[88]`初始化成了`0x58`

然而加上之后，z3依然做不出答案，我们此时可以进一步进行测试，也就是**用预先定义的数据进行初始化，并且和程序对应行号进行对比，确认运算的正确性**。此时可以给python加上代码

```python
if DEBUG:
    flag[7] = ord("b")
    flag[8] = ord("a")
    flag[9] = ord("a")
    flag[10] = ord("a")
    flag[11] = ord("a")
    flag[12] = ord("a")
    flag[13] = ord("a")
    flag[14] = ord("e")
    flag[15] = ord("a")
    flag[16] = ord("a")
    flag[17] = ord("a")

# debug program
tmp = [0]*130
if DEBUG:
    tmp[74] = flag[7] + (flag[8]<<8) + (flag[9]<<16) + (flag[10]<<24)
    tmp[75] = flag[11] + (flag[12]<<8) + (flag[13]<<16) + (flag[14]<<24)
    tmp[76] = flag[15] + (flag[16]<<8) + (flag[17]<<16) + (0x80<<24)

else:
    tmp[74] = Concat(flag[10], flag[9], flag[8], flag[7])
    tmp[75] = Concat(flag[14], flag[13], flag[12], flag[11])
    # 这里进行了修改
    tmp[76] = Concat(BitVecVal(0x80, 8), flag[17], flag[16], flag[15])

print(tmp[74])
print(tmp[76])
# solver.add(tmp[74]+tmp[76] == 1)
tmp[88]=0x58
tmp[89]=0

# mov addr:0x1290
tmp[9]=0xffffffff
# mov addr:0x1370
tmp[125]=0x0
# mov addr:0x1450
tmp[126]=0x0
# mov addr:0x1530
tmp[127]=0x0
# mov addr:0x1610
tmp[128]=0x0
# or addr:0x16f0
tmp[0]=tmp[125]|tmp[8]
# or addr:0x18cf
tmp[1]=tmp[126]|tmp[8]
# or addr:0x1aaf
tmp[2]=tmp[127]|tmp[8]
# or addr:0x1c8f
tmp[3]=tmp[128]|tmp[8]
# mov addr:0x1e6f
tmp[10]=0xd76aa478
# mov addr:0x1f4f
tmp[11]=0xe8c7b756
# mov addr:0x202f
```

此时我们可以用**内存变化**进行调试。也就是我们的python运行到某一行，打印对应的数据，理论上应该和二进制跑出来的答案一致。

根据多次调试可疑点，可以发现，在某一个异或操作之后，逻辑发生了变化。找到对应的汇编，会发现这段汇编有点不同

```php
.text:000000000000BD8C                 mov     [rax+5Fh], cl
.text:000000000000BD8F                 mov     cl, [rax+98h]
.text:000000000000BD95                 or      cl, [rax+118h]
.text:000000000000BD9B                 mov     [rax+0CCh], cl
.text:000000000000BDA1                 mov     cl, [rax+99h]
.text:000000000000BDA7                 or      cl, [rax+119h]
.text:000000000000BDAD                 mov     [rax+0CDh], cl
.text:000000000000BDB3                 mov     cl, [rax+9Ah]
.text:000000000000BDB9                 or      cl, [rax+11Ah]
.text:000000000000BDBF                 mov     [rax+0CEh], cl

;;;;; 跳过部分汇编
.text:000000000000BFA5                 mov     [rax+0C9h], cl
.text:000000000000BFAB                 mov     cl, [rax+86h]
.text:000000000000BFB1                 or      cl, [rax+106h]
.text:000000000000BFB7                 mov     [rax+0CAh], cl
.text:000000000000BFBD                 mov     cl, [rax+87h]
.text:000000000000BFC3                 or      cl, [rax+107h]
.text:000000000000BFC9                 mov     [rax+0CBh], cl
```

仔细观察会发现，代码并非是字字对应的进行或运算，但是有一种**错位对齐的感觉**，根据经验不难判断，这里发生了**循环位移**，笔者这里考虑其进行的循环右移。由于前文提到过，程序实际上是按照32bit的四字节整数在进行运算，此时可以得知

```php
整数tmp下标 = 当前v3下标 //32
```

所以我们这里可以发现，其实当前操作针对的是`tmp[4]`和`tmp[8]`进行操作，并且**并非两个数字的起始位，而是从中间某个位置开始的**。并且同样的，被赋值的`tmp[6]`也并非起始地址。于是通过分析被操作数和操作数的偏移，我们能够得到它是一种类似这样的循环右移的关系

```php
result = (num >> shift_amount) | (num << (32 - shift_amount)) & 0xFFFFFFFF
```

其中，`shift_amount`为被操作数的真实的下标和操作数真实下标计算而来，而这个真实下标`real_offset`算法如下

```php
real_offset = (offset//8)*8+(8-(offset%8))
```

这个offset即为前文提到的被操作数的偏移以及操作数的偏移。

于是，我们能进一步改变我们的dump脚本

```python
def reverse_origin_offset(offset):
    return (offset//8)*8+(8-(offset%8))

def rotate_right(num, shift_amount):
    shift_amount = shift_amount % 32  
    result = (num >> shift_amount) | (num << (32 - shift_amount)) & 0xFFFFFFFF
    return result

if idc.print_insn_mnem(n1) == "xor" and idc.get_operand_type(n1, 0) == 1 and idc.get_operand_type(n1, 1) == 4 and idc.print_insn_mnem(n2) == "mov" and  idc.get_operand_type(n2, 1) == 1:
    #  add or xor
    # xor opreation
    # .text:0000000000005DFE                 mov     cl, [rax+87h]
    # .text:0000000000005E04                 and     cl, [rax+7]
    n4 = idc.next_head(idc.next_head(n2))
    if idc.print_insn_mnem(n4) != "and":
        # xor opreation
        # print("find xor")
        print("# xor addr:"+hex(now_addr))
        r_offset = idc.get_operand_value(n2, 0)
        op1_off = idc.get_operand_value(now_addr, 1)
        op2_off = idc.get_operand_value(n1, 1)
        stack[r_offset//32] =  stack[op1_off//32] ^ stack[op2_off//32]
        print("tmp[%d]=tmp[%d]^tmp[%d]"%(r_offset//32,op1_off//32,op2_off//32))
        for i in range(8*3*4):
            now_addr = idc.next_head(now_addr)
        continue
    else:
        # 0x5DEF~0006831
        # print("find add operation:" + hex(now_addr))
        print("# add addr:"+hex(now_addr))
        op1_off = idc.get_operand_value(now_addr, 1)
        op2_off = idc.get_operand_value(n1, 1)
        r_offset = idc.get_operand_value(n2, 0)
        stack[r_offset//32] =  stack[op1_off//32] + stack[op2_off//32]
        print("tmp[%d]=(tmp[%d]+tmp[%d])%%0x100000000"%(r_offset//32,op1_off//32,op2_off//32))
        for i in range(471):
            now_addr = idc.next_head(now_addr)
        # print("after add addr is "+hex(now_addr))
        continue
```

并且根据这个细节再次改变z3脚本

```python
def rotate_right(num, shift_amount):
    pass
    shift_amount = shift_amount % 32  
    if DEBUG:
        result = (num >> shift_amount) | (num << (32 - shift_amount)) & 0xFFFFFFFF
    else:

result = LShR(num, shift_amount) | (num << (32 - shift_amount))
    return result

# add addr:0x10e3e
tmp[5]=(tmp[4]+tmp[0])%0x100000000
# add addr:0x11886
tmp[6]=(tmp[5]+tmp[77])%0x100000000
# add addr:0x12390
tmp[4]=(tmp[6]+tmp[13])%0x100000000
# or addr:0x12e9a
tmp[0]=tmp[3]|tmp[8]
# or addr:0x13019
tmp[3]=tmp[2]|tmp[8]
# or addr:0x13199
tmp[2]=tmp[1]|tmp[8]
# or addr:0x13319
tmp[6]=rotate_right(tmp[4]|tmp[8],10)
```

最终，我们在**调试模式（也就是指定flag）的情况下，能够得到真实二进制的输出**，此时就是说明当前的算法已经是正确的状态了。于是可以再次使用z3进行运算。

然而，最终z3运行了几个小时，依然得不到结果，仔细考虑算法，会发现程序中存在很多的或与运算，而**与或运算并非一定是可逆的**，这种大量的一对多关系是难以被约束出结果的。于是就意味着我们还得进一步的去理解算法才行。

### 读题：找到真是逻辑

重新回到逻辑，会发现之前忽略了题目中的提示`the recovery key is behind a hasher`，换句话说，这个算法本质上是一个hash算法，并且我们dump出来的数据中存在数个特征值，例如`0xd76aa478`，用这个值尝试搜索，会发现**这个数据其实是md5中的魔数！**重新检查md5也会发现，md5中包含大量的**循环左移**，跟笔者dump的循环右移正好是对应的！也就是说，这个算法本质上是一个md5？

然而，保持之前的对比思想，用一个相同的值放到md5中，会发现得到的答案完全不同，不过根据上网搜到的结果来看，很可能**这个算法并非是完整的md5，而只是一部分**。实际上根据我们dump的逻辑，我们可以发现其就是`md5_transform`这个函数的具体实现

```cpp
static void
md5_transform (const unsigned char block[64])
{
  int i, j;
  UINT4 a,b,c,d,tmp;
  const UINT4 *x = (UINT4 *) block;
  a = state[0];
  b = state[1];
  c = state[2];
  d = state[3];
  /* Round 1 */
  for (i = 0; i < 16; i++)
    {
      tmp = a + F (b, c, d) + le32_to_cpu (x[i]) + T[i];
      tmp = ROTATE_LEFT (tmp, s1[i & 3]);
      tmp += b;
      a = d; d = c; c = b; b = tmp;
    }
  /* Round 2 */
  for (i = 0, j = 1; i < 16; i++, j += 5)
    {
      tmp = a + G (b, c, d) + le32_to_cpu (x[j & 15]) + T[i+16];
      tmp = ROTATE_LEFT (tmp, s2[i & 3]);
      tmp += b;
      a = d; d = c; c = b; b = tmp;
    }
  /* Round 3 */
  for (i = 0, j = 5; i < 16; i++, j += 3)
    {
      tmp = a + H (b, c, d) + le32_to_cpu (x[j & 15]) + T[i+32];
      tmp = ROTATE_LEFT (tmp, s3[i & 3]);
      tmp += b;
      a = d; d = c; c = b; b = tmp;
    }
  /* Round 4 */
  for (i = 0, j = 0; i < 16; i++, j += 7)
    {
      tmp = a + I (b, c, d) + le32_to_cpu (x[j & 15]) + T[i+48];
      tmp = ROTATE_LEFT (tmp, s4[i & 3]);
      tmp += b;
      a = d; d = c; c = b; b = tmp;
    }
  state[0] += a;
  state[1] += b;
  state[2] += c;
  state[3] += d;
}
```

这就是这个题中提到的**hasher**。

### 解题：Cuda爆破

我们回头看前面提到的flag，我们需要得到的有效长度为11字节，但是其中4个字节由约束决定，那么此时需要爆破的长度为7字节，可能行为`62**7`中可能，大概有`1e12`，这个数据量其实非常非常地大，正常情况下比赛期间应该是没办法爆破出来的。然而，市面上有非常多的md5爆破工具，据说都能够较快的进行爆破，通过简单学习会发现，这些爆破工具都是使用了`cuda`进行爆破得到的。那么，我们通过修改这些工具来实现对部分md5的爆破，理论上应该也是可行的。

我这边参考的[repo是这个](https://github.com/iryont/md5-cracker)，我们先准备好对应的[nvdia sdk](https://developer.nvidia.com/cuda-downloads)，然后可以通过修改其操作代码进行爆破。不过要注意几个坑点：

1. cuda进行操作的时候，一定要使用对齐的向量。实际上前文提到的`md5_transform`是不能直接移植的，因为它使用了char直接进行操作（至少笔者搬运代码的时候直接报错了）所以要使用它原生的md5
2. 它的md5会自动帮我们初始化一定的数据，这些数据就包括我们前文提到的`0x80`和`0x58`，然而由于我们的算法和它的爆破逻辑有一点点冲突，需要进行长度方面的修改

首先要记得，我们并非需要初始化全部内容，所以可以修改cuda调用的kernel函数的初始化逻辑

```cpp
char mapping_index[8] = {0,1,2,3,5,6,8};
for (uint32_t hash = 0; hash < HASHES_PER_KERNEL; hash++) {
    for (uint32_t i = 0; i < threadWordLength; i++) {
        threadTextWord[mapping_index[i]] = sharedCharset[threadCharsetWord[i]];
    }

// corctf add 
    threadTextWord[9] = threadTextWord[0] - 1;
    threadTextWord[7] = threadTextWord[9] + 4;
    threadTextWord[10] = threadTextWord[1];
    threadTextWord[4] = threadTextWord[2];

uint32_t threadWordTotalLength = 11;
    md5Hash((unsigned char*)threadTextWord, threadWordTotalLength,&threadHash01, &threadHash02, &threadHash03, &threadHash04);
    if (threadHash03 == hash03 && threadHash04 == hash04) {
        printf("%s\n", threadTextWord);
        memcpy(g_deviceCracked, threadTextWord, threadWordLength);
    }
```

其次，我们的md5中有一些处理是预先处理，与我们输入长度无关，并且`state`也不需要初始化，所以要增加下列修改

```cpp
  int i = 0;
  for(i=0; i < length; i++){
    vals[i / 4] |= data[i] << ((i % 4) * 8);
  }

vals[i / 4] |= 0x80 << ((i % 4) * 8);
  // add here comment
  vals[56 / 4] |= 0x58 << ((56 % 4) * 8);

// at final
  a += a0;
  b += b0;
  c += c0;
  d += d0;
```

然后就能进行爆破了。在等到3h之后，就能得到一个最终的爆破结果，最终就能得到

```php
cPv3v8VfWbP
```

这个要求的数据，将数据输入二进制，就能得到答案

```php
corctf{youtu.be/dQw4w9WgXcQ}
```

这个就是这道题的最终解

总结
--

整个题目做下来一波三折，主要是多次理解错了出题人的意图，导致做题过程非常痛苦，只能不断使用对比的方式来纠正思路。这几年的逆向题越来越不能通过硬做的方式来获取答案，而得学会合理的使用各种工具来辅助分析和解题，才能在比赛期间完成题目。

发表于 2024-08-16 09:00:02
阅读 ( 1511 )
分类：其他

CorCTF 2024 Rev DigestMe

0 条评论