问答
发起
提问
文章
攻防
活动
Toggle navigation
首页
(current)
问答
商城
实战攻防技术
活动
摸鱼办
搜索
登录
注册
对抗样本生成技术分析与实现2
漏洞分析
在继续分析、实现其他经典对抗样本技术之前,我们先来看看对抗样本在网络空间安全其他领域的广泛应用。
网安应用 ==== 在继续分析、实现其他经典对抗样本技术之前,我们先来看看对抗样本在网络空间安全其他领域的广泛应用。 在恶意软件方面,通过对恶意软件样本添加对抗扰动,使其在特征空间中发生微小变化,从而躲避基于机器学习的恶意软件检测引擎。另外,利用对抗样本生成技术,可以从已知的恶意软件样本中生成新的、具有对抗性的恶意软件变种,增加检测难度。 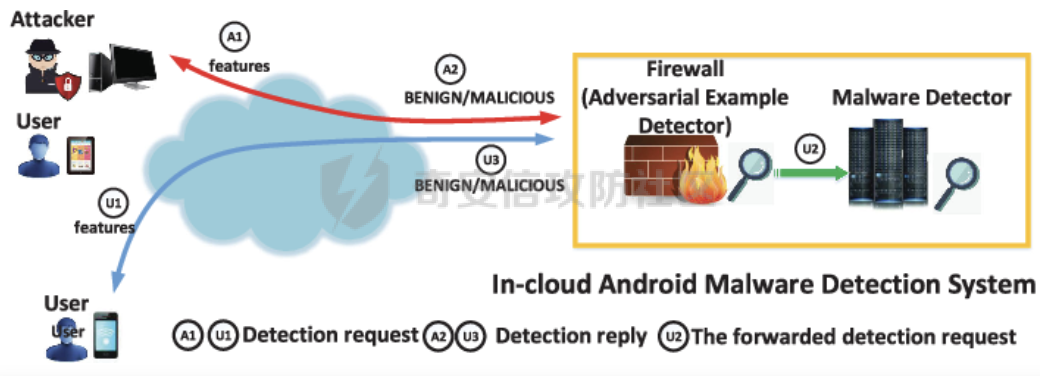 在入侵检测方面,通过构造对抗性的网络流量,可以欺骗入侵检测系统,使其无法识别出真正的入侵行为。另外,对抗样本可以诱导入侵检测系统做出错误的响应,例如发出误报或漏报,从而影响安全防护效果。 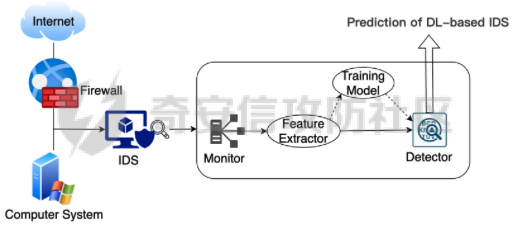 在物联网安全方面, 通过向智能设备发送对抗样本,可以误导设备的传感器或控制系统,从而实现对设备的控制。另外,对抗样本可以用于攻击智能家居系统中的语音助手、智能摄像头等设备,窃取用户隐私或控制家庭设备。 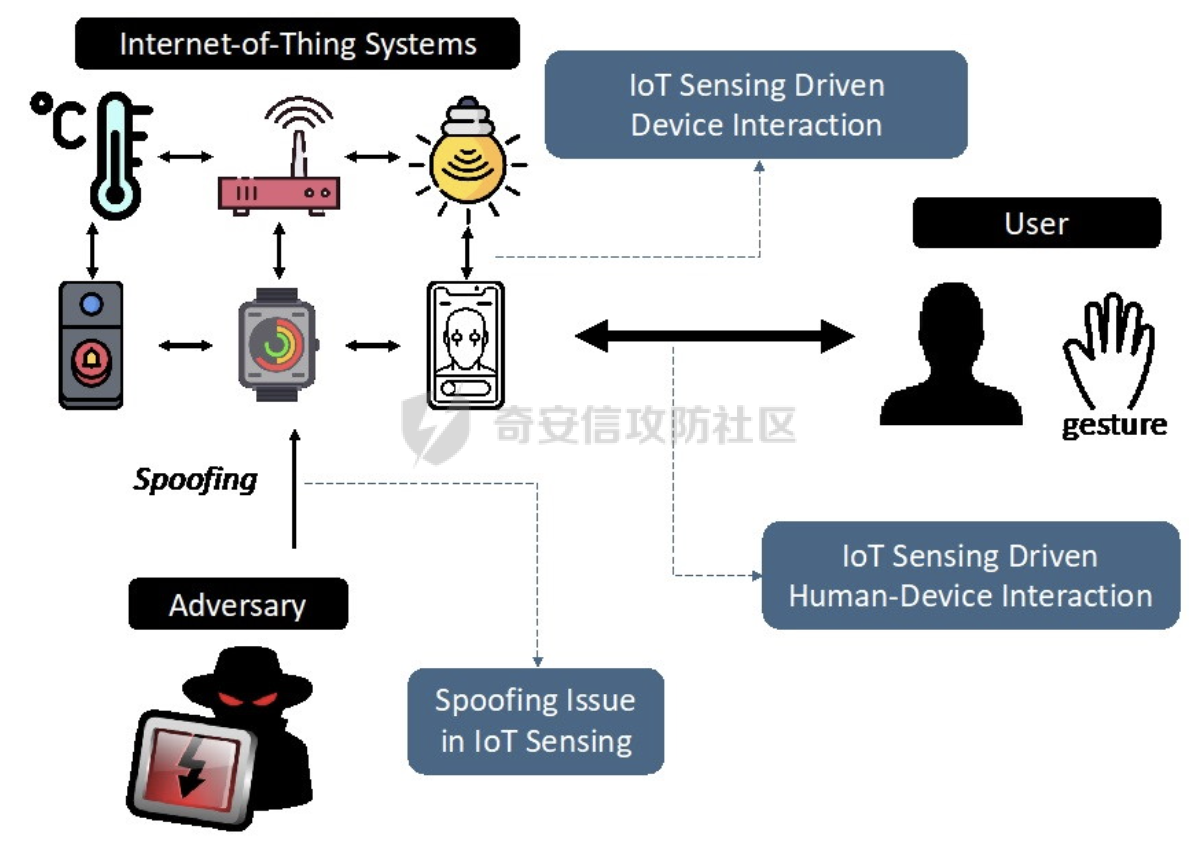 在网站安全方面, 利用对抗样本生成技术,可以生成具有高度欺骗性的钓鱼邮件,诱导用户点击恶意链接或下载恶意软件。另外对抗样本也可以帮助攻击者绕过基于机器学习的反钓鱼系统,提高钓鱼攻击的成功率。 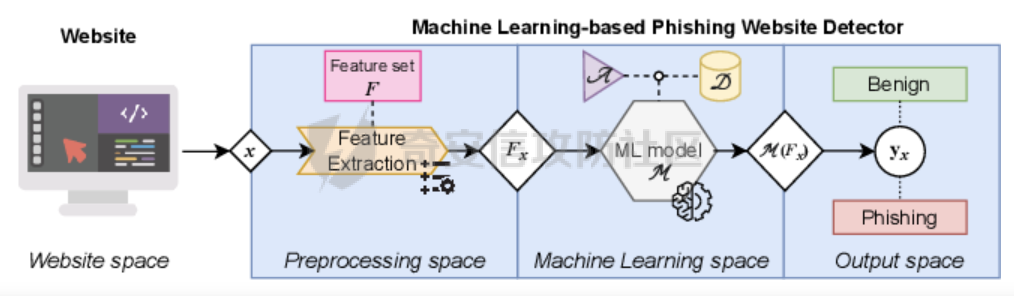 其外在很多其他子领域也有对抗样本的身影,这里不再一一赘述。 现在我们继续来学习其他经典的对抗攻击方法。 PGD === 理论 -- PGD方法来自另一篇经典的论文《Towards Deep Learning Models Resistant to Adversarial Attacks》。针对对抗攻击,以往的研究提出了多种防御机制,例如防御性蒸馏(defensive distillation)、特征压缩(feature squeezing)等方法,这些方法在提高模型对特定攻击的鲁棒性方面取得了一定的进展,但它们通常缺乏对所提供保证的深入理解,无法确保模型能够抵御所有可能的对抗性攻击。 本文提出了一种基于鲁棒优化(robust optimization)的新视角来研究神经网络的对抗性鲁棒性。这种方法不仅为我们提供了一个统一的框架来理解以往的工作,而且通过其原则性的特点,使我们能够识别出既可靠又在某种意义上通用的训练和攻击神经网络的方法。具体来说,本文的方法通过一个自然的鞍点(min-max)公式来精确地定义对对抗性攻击的安全保证,即我们希望模型能够抵抗的攻击类型。 与以往方法的一个关键区别在于,本文不仅关注于提高对特定已知攻击的鲁棒性,而是首先提出了一个具体的安全保证,然后调整训练方法以实现这一保证。这涉及到对攻击模型的精确定义,即明确我们的模型应该能够抵抗的攻击类型。本文中,作者选择了范数球来形式化敌手的操作能力,这是一种自然的方式来定义图像之间的感知相似性。 本文的方法通过实验研究了鞍点公式所对应的优化景观,发现尽管其组成部分是非凸的且非凹的,但在实践中,该优化问题是可行的。特别是,作者提供了强有力的证据表明,一阶方法可以可靠地解决这个问题。此外,作者还探讨了网络架构对对抗性鲁棒性的影响,发现模型容量在其中起着重要作用。为了可靠地抵御强大的对抗性攻击,网络需要比仅对良性示例进行正确分类的模型具有更大的容量。 我们来形式化该方案。本文的核心方法是基于鲁棒优化理论来增强深度学习模型对于对抗性攻击的抵抗力。具体而言,作者采用了一个鞍点问题(min-max problem)的数学框架来形式化和解决这个问题。下面是对本文方法的数学描述和分析: 1. **问题设置**: 假设我们有一个数据分布 ( D ),它产生样本对 ( (x, y) ),其中 ( x ) 是输入数据,( y ) 是对应的标签。我们的目标是找到一组模型参数 ( \\theta ),使得在分布 ( D ) 下的期望损失最小化。然而,传统的经验风险最小化(ERM)方法并不保证模型对对抗性攻击的鲁棒性。 2. **鞍点公式**: 为了解决这个问题,本文引入了一个鞍点问题,定义了一个鲁棒的风险函数 ( \\rho(\\theta) ): 其中,( L ) 是损失函数(例如交叉熵损失),( S ) 是允许的扰动集合,它定义了对抗性攻击的范围。 3. **优化视角**: 上述鞍点问题可以分解为两个部分:内部最大化问题和外部最小化问题。内部最大化问题旨在找到给定数据点 ( x ) 的对抗性版本 ( x + \\delta ),使得损失函数 ( L ) 最大化。外部最小化问题则是寻找模型参数 ( \\theta ),使得在考虑内部攻击问题的情况下,期望损失最小化。 4. **对抗性训练**: 对抗性训练可以看作是解决上述鞍点问题的一种方法。具体来说,可以通过投影梯度下降(PGD)来近似解决内部最大化问题,从而找到对抗性样本。然后,使用这些对抗性样本来训练网络,使得外部最小化问题得以解决。 在攻击实现上,相当于攻击执行 `nb_iter` 次步长为 `eps_iter` 的步骤,同时始终保持在距离初始点 `eps` 以内。 实现 -- 这段代码定义了一个名为`PGDAttack`的类,实现了一种称为投影梯度下降(PGD)的对抗攻击方法。通过创建该类的实例并调用其`perturb`方法,可以对输入数据进行对抗攻击,生成对抗样本。 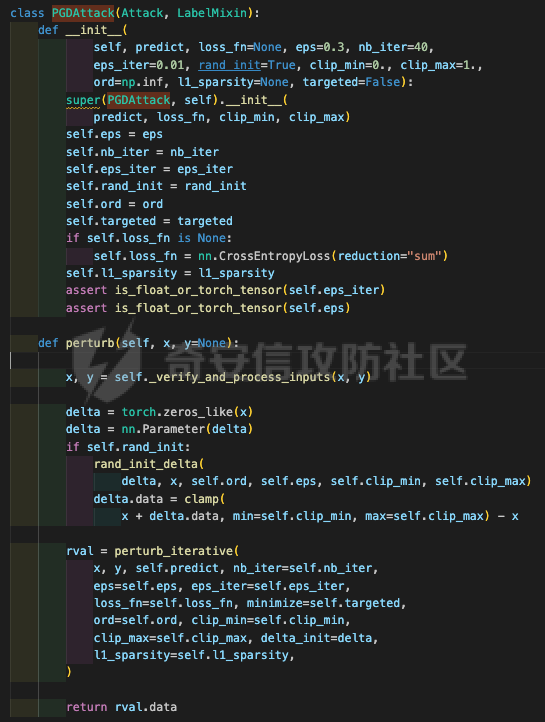 这段代码定义了一个名为`PGDAttack`的类,它继承自`Attack`和`LabelMixin`两个类。这个类实现了一种称为投影梯度下降(Projected Gradient Descent,简称PGD)的对抗攻击方法。 1. `__init__`方法:这是类的构造函数,用于初始化类的实例。 - `predict`:输入模型的预测函数。 - `loss_fn`:损失函数,默认为`None`。 - `eps`:攻击强度,默认为0.3。 - `nb_iter`:迭代次数,默认为40。 - `eps_iter`:每次迭代的攻击强度,默认为0.01。 - `rand_init`:布尔值,表示是否随机初始化扰动,默认为`True`。 - `clip_min`和`clip_max`:用于限制输入数据的范围,默认分别为0和1。 - `ord`:范数类型,默认为`np.inf`。 - `l1_sparsity`:L1稀疏性约束,默认为`None`。 - `targeted`:布尔值,表示攻击是否针对特定目标类别。 在构造函数中,首先调用父类的构造函数,并将`predict`、`loss_fn`、`clip_min`和`clip_max`作为参数传递。然后设置其他属性。如果`loss_fn`为`None`,则将其设置为`nn.CrossEntropyLoss(reduction="sum")`。最后,检查`eps_iter`和`eps`是否为浮点数或张量。 2. `perturb`方法:这是实际执行对抗攻击的方法。 - 输入参数`x`和`y`分别表示原始输入数据和对应的标签。 - 使用`_verify_and_process_inputs`方法验证和处理输入数据。 - 创建一个与`x`形状相同的零张量`delta`,并将其转换为`nn.Parameter`类型。 - 如果`rand_init`为`True`,则使用`rand_init_delta`函数随机初始化扰动。 - 调用`perturb_iterative`函数进行迭代攻击,返回对抗样本`rval`。 - 返回处理后的对抗样本`rval.data`。 执行攻击,效果如下  将大熊猫预测为了开关 PGD在L无穷范数下进行 如下代码定义了一个名为`LinfPGDAttack`的类,实现了一种基于L∞范数的PGD对抗攻击方法。通过创建该类的实例,可以对输入数据进行对抗攻击,生成对抗样本。 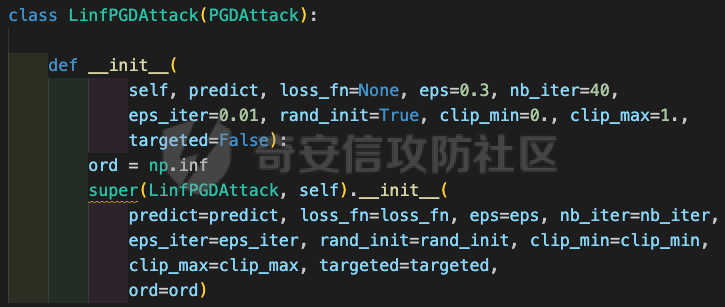 这段代码定义了一个名为`LinfPGDAttack`的类,它继承自`PGDAttack`类。这个类实现了一种基于L∞范数的PGD(投影梯度下降)对抗攻击方法。 1. `__init__`方法:这是类的构造函数,用于初始化类的实例。 - `predict`:输入模型的预测函数。 - `loss_fn`:损失函数,默认为`None`。 - `eps`:攻击强度,默认为0.3。 - `nb_iter`:迭代次数,默认为40。 - `eps_iter`:每次迭代的攻击强度,默认为0.01。 - `rand_init`:布尔值,表示是否随机初始化扰动,默认为`True`。 - `clip_min`和`clip_max`:用于限制输入数据的范围,默认分别为0和1。 - `targeted`:布尔值,表示攻击是否针对特定目标类别。 在构造函数中,首先设置范数类型`ord=np.inf`,表示使用L∞范数。然后调用父类`PGDAttack`的构造函数,并将所有参数传递给它。 执行效果如下 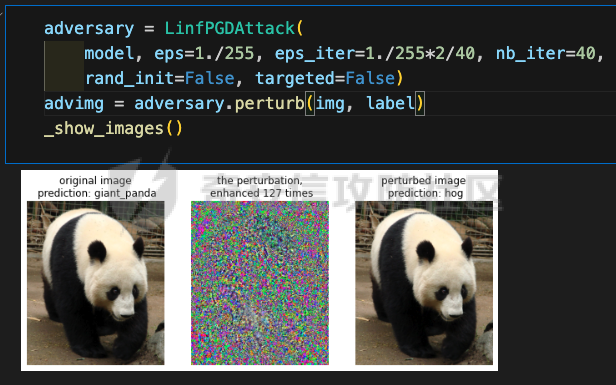 将大熊猫预测为了猪 PGD也可以在L2范数下进行 如下代码定义了一个名为`L2PGDAttack`的类,实现了一种基于L2范数的PGD对抗攻击方法。通过创建该类的实例,可以对输入数据进行对抗攻击,生成对抗样本。 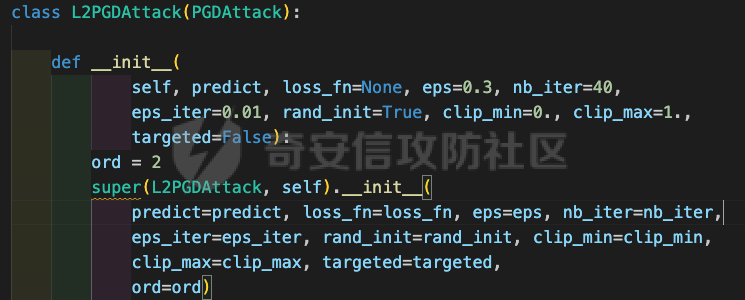 这段代码定义了一个名为`L2PGDAttack`的类,它继承自`PGDAttack`类。这个类实现了一种基于L2范数的PGD(投影梯度下降)对抗攻击方法。 1. `__init__`方法:这是类的构造函数,用于初始化类的实例。 - `predict`:输入模型的预测函数。 - `loss_fn`:损失函数,默认为`None`。 - `eps`:攻击强度,默认为0.3。 - `nb_iter`:迭代次数,默认为40。 - `eps_iter`:每次迭代的攻击强度,默认为0.01。 - `rand_init`:布尔值,表示是否随机初始化扰动,默认为`True`。 - `clip_min`和`clip_max`:用于限制输入数据的范围,默认分别为0和1。 - `targeted`:布尔值,表示攻击是否针对特定目标类别。 在构造函数中,首先设置范数类型`ord=2`,表示使用L2范数。然后调用父类`PGDAttack`的构造函数,并将所有参数传递给它。 攻击效果如下 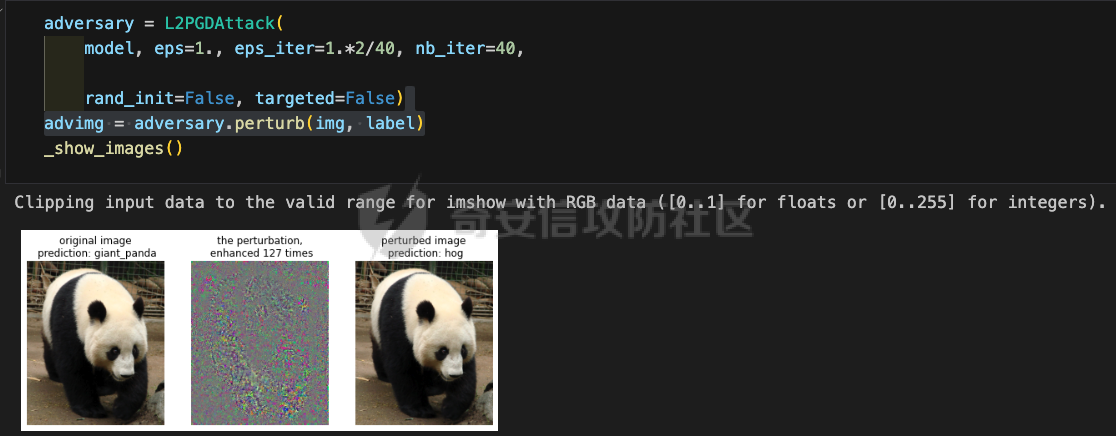 可以看到,将大熊猫预测为了猪。 MomentumIterativeAttack ======================= 理论 -- 传统的对抗性攻击方法主要关注在白盒模型上生成对抗样本,这些样本通过在合法输入中添加微小的、人类难以察觉的噪声来误导模型做出错误的预测。然而,这些方法在黑盒模型上的应用效果并不理想,特别是在模型具有防御机制时,攻击成功率会显著下降。 MomentumIterativeAttack是一种基于动量的迭代算法,用以增强对抗性攻击的力度。这种方法通过在迭代过程中整合动量项,可以稳定更新方向,并帮助算法从局部最优解中逃逸,从而生成更具迁移性的对抗样本。具体来说,该方法不仅提高了在白盒模型上的攻击成功率,而且在黑盒模型上也表现出色,即使是经过强化训练、具备强大防御能力的模型,也可能对我们的黑盒攻击无能为力。 与现有方法相比,动量迭代梯度基方法(Momentum Iterative Gradient-based Methods)有几个显著的不同之处。首先,它通过积累跨迭代的梯度方向的动量向量,增强了对抗样本的迁移性。其次,该方法不仅针对单一模型,还研究了如何同时攻击多个模型的集成方法,进一步增强了对抗样本的迁移性。 如下是论文中应用该方案得到的对抗样本的示意图  现在我们来形式化该方案 基于动量的迭代梯度符号方法(Momentum Iterative Fast Gradient Sign Method, MI-FGSM),其核心思想是在迭代过程中引入动量(momentum)来增强对抗样本的生成过程。具体来说,这种方法通过以下数学公式来实现: 1. **初始化**:选择一个合法的输入样本 ( x ) 和其正确的标签 ( y ),设定扰动大小 ( \\epsilon ),迭代次数 ( T ),以及衰减因子 ( \\mu )。 2. **迭代过程**:在每次迭代 ( t ) 中,执行以下步骤: - 计算当前样本 ( x^\*\_t ) 对于模型的损失函数 的梯度。 - 更新动量向量 ( g\_{t+1} ),该向量是之前动量 ( g\_t ) 与当前梯度的加权和: - 生成对抗样本 ( x^\*\_{t+1} ),通过将当前样本 ( x^\**t ) 与动量向量 ( g*{t+1} ) 的符号相结合,并缩放一个步长 ( \\alpha )(( \\alpha = \\frac{\\epsilon}{T} )): 3. **输出**:在完成 ( T ) 次迭代后,输出最终的对抗样本 这种方法与以往的对抗性攻击方法相比,主要有以下不同之处: - **动量的引入**:通过积累之前迭代的梯度信息,增强了对抗样本在不同迭代间的一致性,有助于避免陷入局部最优解,提高了对抗样本的迁移性。 - **衰减因子 ( \\mu )**:该因子控制了历史梯度信息在动量向量中的权重,对于平衡攻击的强度和迁移性至关重要。 - **迭代攻击**:与一步攻击(如FGSM)相比,迭代方法通过多次更新对抗样本,可以更精细地逼近模型的决策边界,从而提高攻击成功率。 - **对多个模型的攻击**:本文还探讨了如何通过集成多个模型的输出(例如,通过融合模型的对数几率)来生成对抗样本,这进一步提高了对抗样本的迁移性和攻击的成功率。 通过这些数学公式和方法的结合,本文提出的方案在理论和实验上都显示出了对现有对抗性攻击方法的显著改进,特别是在黑盒攻击场景中。 实现 -- 如下代码定义了一个名为`MomentumIterativeAttack`的类,实现了一种带有动量的迭代对抗攻击方法。通过创建该类的实例并调用其`perturb`方法,可以对输入数据进行对抗攻击,生成对抗样本。 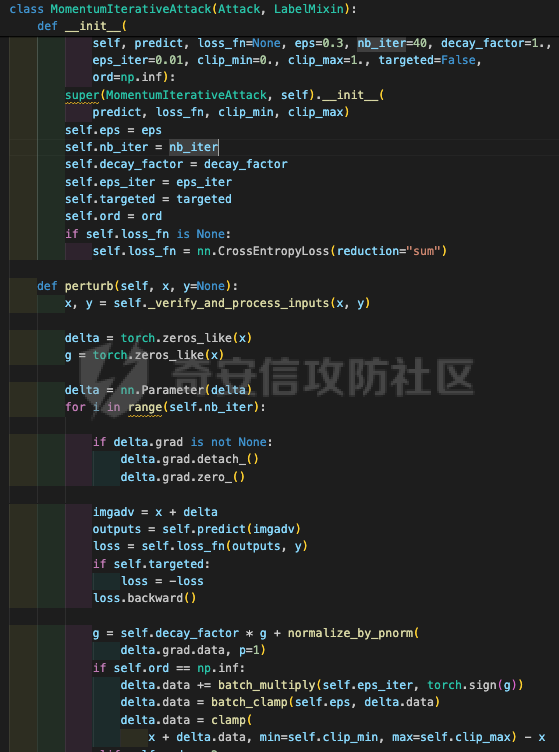 这段代码定义了一个名为`MomentumIterativeAttack`的类,它继承自`Attack`和`LabelMixin`两个类。这个类实现了一种带有动量的迭代对抗攻击方法。 1. `__init__`方法:这是类的构造函数,用于初始化类的实例。 - `predict`:输入模型的预测函数。 - `loss_fn`:损失函数,默认为`None`。 - `eps`:攻击强度,默认为0.3。 - `nb_iter`:迭代次数,默认为40。 - `decay_factor`:动量衰减因子,默认为1.0。 - `eps_iter`:每次迭代的攻击强度,默认为0.01。 - `clip_min`和`clip_max`:用于限制输入数据的范围,默认分别为0和1。 - `targeted`:布尔值,表示攻击是否针对特定目标类别。 - `ord`:范数类型,默认为`np.inf`。 在构造函数中,首先调用父类的构造函数,并将`predict`、`loss_fn`、`clip_min`和`clip_max`作为参数传递。然后设置其他属性。如果`loss_fn`为`None`,则将其设置为`nn.CrossEntropyLoss(reduction="sum")`。 2. `perturb`方法:这是实际执行对抗攻击的方法。 - 输入参数`x`和`y`分别表示原始输入数据和对应的标签。 - 使用`_verify_and_process_inputs`方法验证和处理输入数据。 - 创建一个与`x`形状相同的零张量`delta`和一个相同形状的零张量`g`,并将`delta`转换为`nn.Parameter`类型。 - 对于每次迭代: 1. 如果`delta.grad`不为`None`,则将其分离并清零。 2. 计算当前扰动下的对抗样本`imgadv`。 3. 将`imgadv`输入到模型中,得到预测结果`outputs`。 4. 计算损失`loss`,如果`targeted`为`True`,则取负值。 5. 对损失进行反向传播。 6. 更新动量`g`。 7. 根据范数类型`ord`更新扰动`delta`。 - 返回处理后的对抗样本`rval`。 执行攻击如下 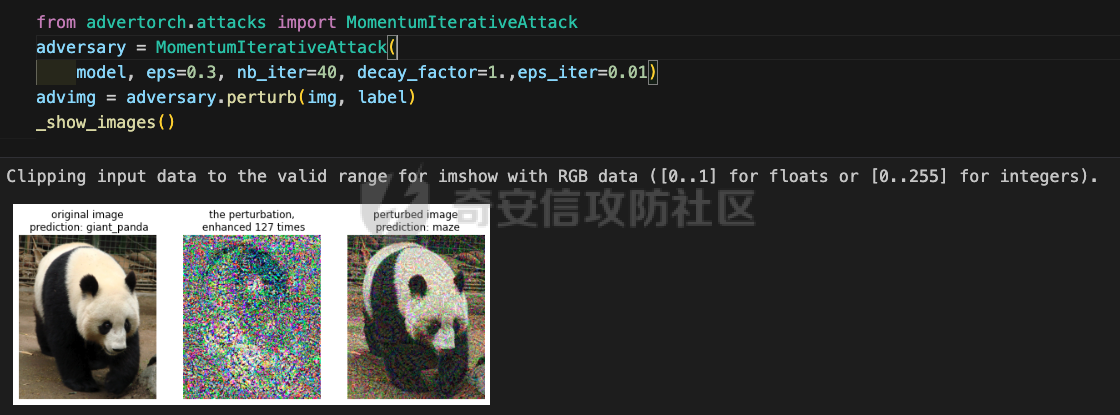 在上图可以看到,将大熊猫错误地识别为了迷宫 也可以在L2范数下进行 如下代码定义了一个名为`L2MomentumIterativeAttack`的类,实现了一种基于L2范数的带有动量的迭代对抗攻击方法。通过创建该类的实例,可以对输入数据进行对抗攻击,生成对抗样本。 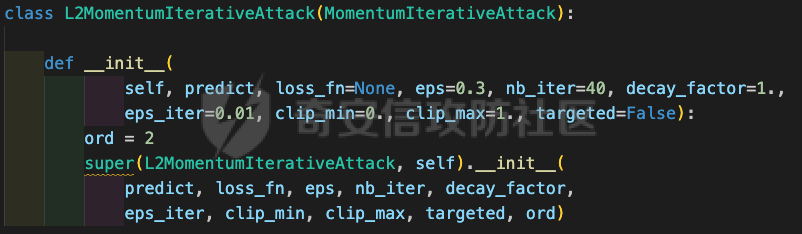 这段代码定义了一个名为`L2MomentumIterativeAttack`的类,它继承自`MomentumIterativeAttack`类。这个类实现了一种基于L2范数的带有动量的迭代对抗攻击方法。 1. `__init__`方法:这是类的构造函数,用于初始化类的实例。 - `predict`:输入模型的预测函数。 - `loss_fn`:损失函数,默认为`None`。 - `eps`:攻击强度,默认为0.3。 - `nb_iter`:迭代次数,默认为40。 - `decay_factor`:动量衰减因子,默认为1.0。 - `eps_iter`:每次迭代的攻击强度,默认为0.01。 - `clip_min`和`clip_max`:用于限制输入数据的范围,默认分别为0和1。 - `targeted`:布尔值,表示攻击是否针对特定目标类别。 在构造函数中,首先设置范数类型`ord=2`,表示使用L2范数。然后调用父类`MomentumIterativeAttack`的构造函数,并将所有参数传递给它。 进行攻击后,结果如下,将大熊猫识别为了猪 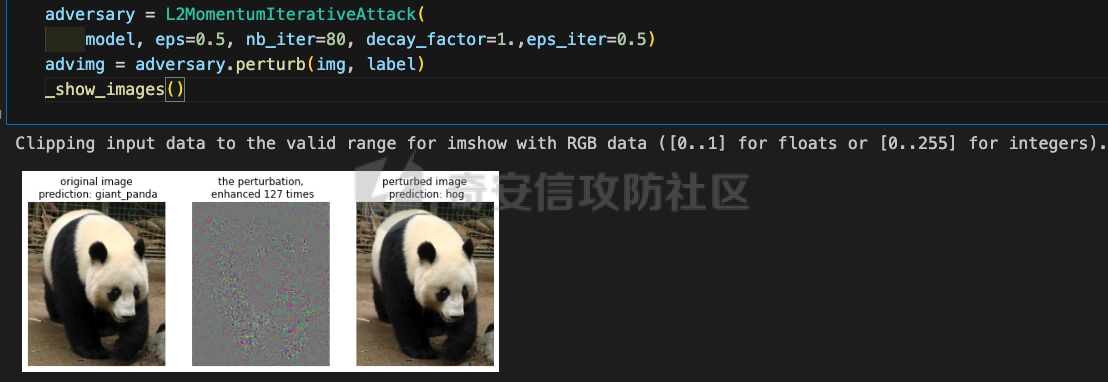 也可以在L无穷范数下进行 如下代码定义了一个名为`LinfMomentumIterativeAttack`的类,实现了一种基于L∞范数的带有动量的迭代对抗攻击方法。通过创建该类的实例,可以对输入数据进行对抗攻击,生成对抗样本。 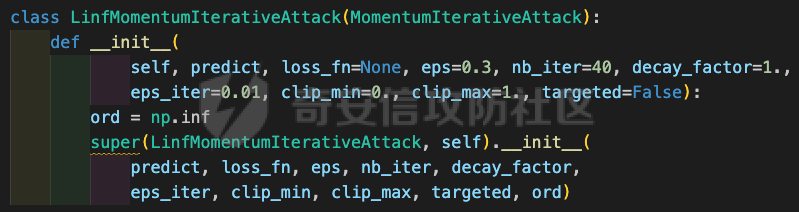 这段代码定义了一个名为`LinfMomentumIterativeAttack`的类,它继承自`MomentumIterativeAttack`类。这个类实现了一种基于L∞范数的带有动量的迭代对抗攻击方法。 `__init__`方法:这是类的构造函数,用于初始化类的实例。 - `predict`:输入模型的预测函数。 - `loss_fn`:损失函数,默认为`None`。 - `eps`:攻击强度,默认为0.3。 - `nb_iter`:迭代次数,默认为40。 - `decay_factor`:动量衰减因子,默认为1.0。 - `eps_iter`:每次迭代的攻击强度,默认为0.01。 - `clip_min`和`clip_max`:用于限制输入数据的范围,默认分别为0和1。 - `targeted`:布尔值,表示攻击是否针对特定目标类别。 在构造函数中,首先设置范数类型`ord=np.inf`,表示使用L∞范数。然后调用父类`MomentumIterativeAttack`的构造函数,并将所有参数传递给它。 执行后如下所示,通过攻击,模型会将大熊猫错误识别为泡沫 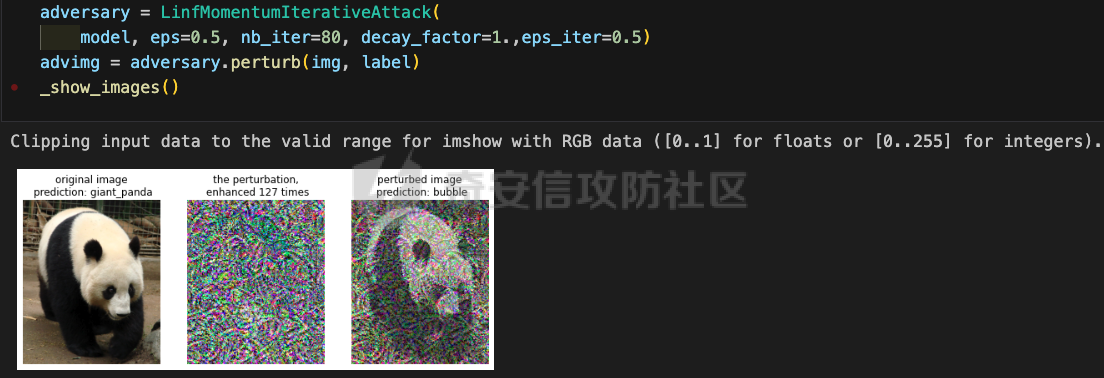 SPSA ==== 这一攻击方法出自《Adversarial Risk and the Dangers of Evaluating Against Weak Attacks》,其实本身主要探讨了对抗性攻击和评估对抗性鲁棒性的方法 在深度学习领域,尽管取得了显著的成功,但研究人员发现神经网络对某些小的输入扰动非常敏感。这些扰动被称为对抗性示例,它们可以导致神经网络产生极其错误的结果。为了防御这些攻击,研究者们提出了多种方法,如通过优化方法找到最大化网络损失的扰动。然而,这些方法往往依赖于特定的攻击方式和评估指标,可能无法全面评估模型的鲁棒性。 这个工作提出了“对抗性风险”这一概念,将其作为实现对最坏情况输入鲁棒模型的目标。作者指出,常用的攻击和评估指标实际上定义了一个可行的替代目标,而不是真正的对抗性风险。这可能导致模型优化这个替代目标,而不是真正的对抗性风险。文章引入了“对敌隐蔽性”这一概念,并开发了工具和启发式方法来识别隐蔽模型并设计透明模型。 我们来形式化本文提出的对抗样本构造方法 SPSA(Simultaneous Perturbation Stochastic Approximation)是一种用于优化高维问题的方法,特别适用于当无法直接获得梯度信息时。在构造对抗样本的背景下,SPSA可以用来近似目标函数的梯度,进而找到最大化损失函数的输入扰动。 1. **初始化**:选择初始图像 ( x\_0 ) 和一个较小的扰动大小 ( \\delta )。 2. **定义目标函数**:目标函数 ( f ) 是模型的损失函数,通常是希望被最大化的,以便找到导致模型误分类的输入点。 3. **迭代过程**: - 对于每次迭代 - 随机采样一个批量 ( n ) 个扰动向量 ( v\_1, \\ldots, v\_n ),这些向量是从 中独立同分布采样得到的。 - 计算每个扰动向量 ( v\_i ) 对目标函数 ( f ) 的影响: - 使用这些影响来估计梯度: - 更新当前图像 ( x\_t ): - 将更新后的图像 ( x'*t ) 投影回 ( \\ell*\\infty ) 范数球内,确保满足原始的约束条件: 4. **参数选择**: - 步长 ( \\alpha ):控制每次迭代更新的幅度。 - 扰动大小 ( \\delta ):控制扰动向量的大小,影响梯度估计的精度。 5. **终止条件**:迭代 ( T ) 次或者达到其他预设的终止条件。 6. **输出**:最终的图像 ( x\_T ) 就是所求的对抗样本。 SPSA方法的核心在于使用随机扰动来估计梯度,这种方法不需要模型的梯度信息,因此在处理非微分或难以微分的模型时特别有用。在对抗样本的构造中,SPSA可以有效地找到那些导致模型出错的输入扰动,即使在模型防御措施(如输入变换或非微分操作)使得传统基于梯度的攻击方法失效的情况下。 实现 -- 如下两个函数通常在深度学习中的对抗训练或对抗攻击等场景中使用,用于处理梯度和数据的批量处理。  ### linf\_clamp\_ 这个函数用于对输入的梯度 `dx` 进行裁剪,以确保在应用这些梯度后,输入数据 `x` 的变化不会超过某个阈值 `eps`。同时,它还会确保新的输入数据 `x_adv` 保持在指定的范围内(由 `clip_min` 和 `clip_max` 定义)。 函数参数: - `dx`:输入的梯度张量。 - `x`:原始输入数据张量。 - `eps`:允许的最大变化量。 - `clip_min` 和 `clip_max`:新输入数据的最小和最大允许值。 函数返回值: - `dx`:裁剪后的梯度张量。 函数实现步骤: 1. 使用 `batch_clamp` 函数将梯度 `dx` 裁剪到 `[-eps, eps]` 范围内。 2. 计算新的输入数据 `x_adv`,即原始输入数据 `x` 加上裁剪后的梯度 `dx_clamped`。 3. 确保 `x_adv` 保持在 `[clip_min, clip_max]` 范围内。 4. 更新梯度 `dx`,使其等于 `x_adv - x - dx`,即新的梯度应该使得 `x_adv = x + dx`。 5. 返回更新后的梯度 `dx`。 ### \_get\_batch\_sizes 这个函数用于计算将一组数据分成多个批次时,每个批次的大小。 函数参数: - `n`:数据的总数。 - `max_batch_size`:每个批次的最大大小。 函数返回值: - 一个列表,包含每个批次的大小。 函数实现步骤: 1. 计算可以完整分成的批次数量,即 `n // max_batch_size`,并为这些批次分配 `max_batch_size`。 2. 如果数据的总数 `n` 不能被 `max_batch_size` 整除,那么最后一个批次的大小将是 `n % max_batch_size`。 3. 返回包含所有批次大小的列表。 如下函数可以用于优化问题,特别是在梯度计算成本较高或难以计算的情况下。 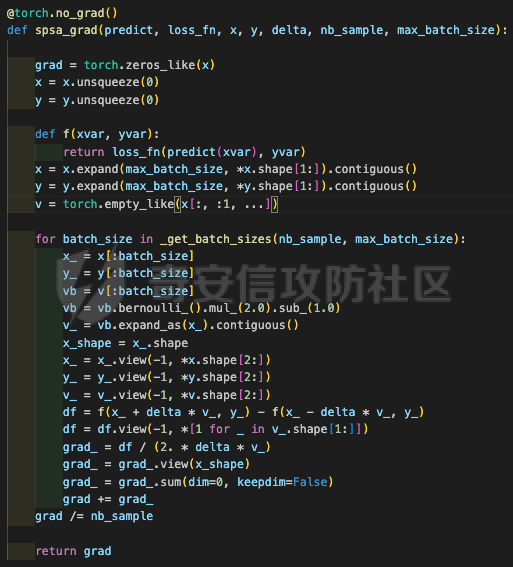 这段代码定义了一个名为`spsa_grad`的函数,它使用随机采样策略(Simultaneous Perturbation Stochastic Approximation,SPSA)来估计梯度。SPSA是一种用于优化和求解梯度的方法,特别适用于大规模问题,因为它不需要计算完整的梯度。 函数参数: - `predict`:输入模型的预测函数。 - `loss_fn`:损失函数。 - `x`:输入数据张量。 - `y`:目标标签张量。 - `delta`:SPSA算法中的参数,用于控制扰动的大小。 - `nb_sample`:用于估计梯度的样本数量。 - `max_batch_size`:每个批次的最大大小。 函数返回值: - `grad`:估计的梯度张量。 函数实现步骤: 1. 使用`torch.no_grad()`上下文管理器,确保在计算过程中不跟踪梯度。 2. 初始化梯度张量`grad`为零张量,形状与输入数据`x`相同。 3. 将输入数据`x`和目标标签`y`扩展为形状为`(max_batch_size, *x.shape[1:])`的张量。 4. 定义一个内部函数`f(xvar, yvar)`,用于计算给定输入和目标标签的损失值。 5. 对于每个批次大小,执行以下操作: 1. 选择当前批次的数据`x_`和`y_`。 2. 生成与`x_`形状相同的伯努利分布随机张量`vb`,并将其值缩放到`[-1, 1]`范围内。 3. 将`vb`扩展为与`x_`相同的形状,并计算扰动张量`v_`。 4. 计算正向和负向扰动下的损失值之差`df`。 5. 将`df`调整为与`v_`相同的形状,并计算梯度估计`grad_`。 6. 将`grad_`累加到总梯度`grad`中。 6. 将总梯度`grad`除以样本数量`nb_sample`,以获得平均梯度。 7. 返回估计的梯度`grad`。 如下函数结合了SPSA梯度估计和优化器,以生成对抗样本。这种方法可以在梯度计算成本较高或难以计算的情况下,有效地生成对抗样本。 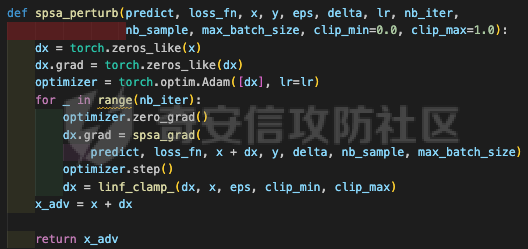 这段代码定义了一个名为`spsa_perturb`的函数,它使用SPSA梯度估计和优化器来生成对抗样本。 函数参数: - `predict`:输入模型的预测函数。 - `loss_fn`:损失函数。 - `x`:输入数据张量。 - `y`:目标标签张量。 - `eps`:允许的最大变化量。 - `delta`:SPSA算法中的参数,用于控制扰动的大小。 - `lr`:优化器的学习率。 - `nb_iter`:优化器的迭代次数。 - `nb_sample`:用于估计梯度的样本数量。 - `max_batch_size`:每个批次的最大大小。 - `clip_min`和`clip_max`:用于限制对抗样本的范围。 函数返回值: - `x_adv`:生成的对抗样本。 函数实现步骤: 1. 初始化扰动张量`dx`为零张量,形状与输入数据`x`相同,并为其设置梯度。 2. 创建一个Adam优化器,用于更新扰动张量`dx`。 3. 对于每次迭代: 1. 清空优化器的梯度。 2. 使用`spsa_grad`函数计算扰动张量`dx`的梯度。 3. 使用优化器更新扰动张量`dx`。 4. 使用`linf_clamp_`函数将扰动张量`dx`限制在`[-eps, eps]`范围内,并确保新的输入数据`x_adv`保持在`[clip_min, clip_max]`范围内。 4. 返回生成的对抗样本`x_adv`。 如下的`LinfSPSAAttack`类提供了一种在L∞范数约束下对深度神经网络进行攻击的方法,它可以用于评估模型的鲁棒性或者生成对抗样本。 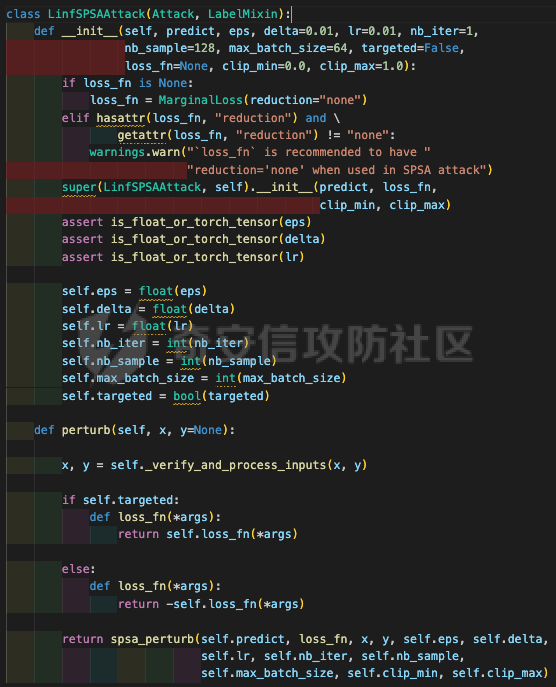 这个类是用来执行针对深度神经网络的L∞范数空间下的SPSA(Simultaneous Perturbation Stochastic Approximation)攻击的。SPSA是一种基于梯度的优化算法,用于在不知道目标函数的梯度的情况下最小化或最大化该函数。 1. **初始化方法 (`__init__`)**: - 接受多个参数,包括预测函数(通常是神经网络)、最大扰动量(`eps`)、扰动的尺度参数(`delta`)、学习率(`lr`)、迭代次数(`nb_iter`)、每次迭代的样本数量(`nb_sample`)、最大批量大小(`max_batch_size`)、是否针对特定目标(`targeted`)、损失函数(`loss_fn`)以及输入数据的裁剪范围(`clip_min`和`clip_max`)。 - 如果没有提供损失函数,则默认使用`MarginalLoss`,并且设置`reduction="none"`,这意味着损失函数将为每个样本返回一个单独的损失值,而不是平均值。 - 对输入参数进行类型检查,确保它们是浮点数或PyTorch张量,并将它们转换为适当的类型。 - 将所有参数存储为类的属性。 2. **扰动方法 (`perturb`)**: - 这个方法用于实际执行攻击,它接受原始输入数据(`x`)和目标标签(`y`,如果有的话)。 - 首先验证并处理输入数据。 - 根据攻击是否针对特定目标,定义损失函数。如果攻击是针对性的,损失函数保持不变;如果不是针对性的,损失函数取负值,因为目标是使损失最大化。 - 调用`spsa_perturb`函数来执行实际的扰动过程。这个函数会返回经过扰动的输入数据,这些数据被设计为在给定的扰动范围内尽可能地误导预测函数。 `spsa_perturb`函数是SPSA算法的核心,它通过在每次迭代中对输入数据进行小的随机扰动,并根据损失函数的变化来调整扰动的方向和大小,从而逐步逼近最优扰动。 进行对抗攻击,效果如下 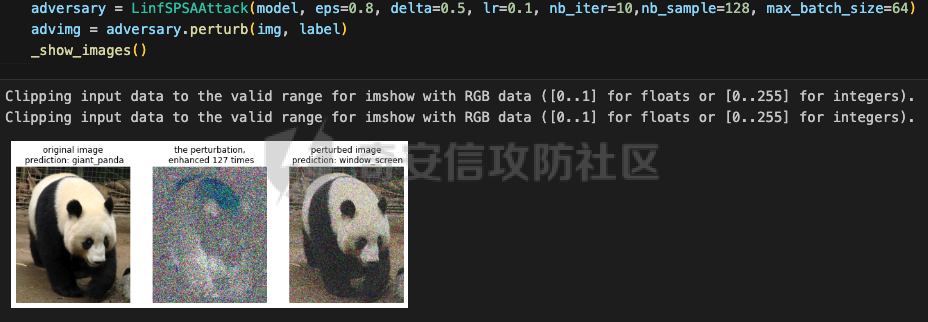 可以看到,将大熊猫预测为了窗户 参考 == 1.<https://arxiv.org/pdf/1710.06081> 2.<https://arxiv.org/pdf/1802.05666> [https://link.springer.com/chapter/10.1007/978-3-319-66399-9\_4](https://link.springer.com/chapter/10.1007/978-3-319-66399-9_4) 4.<https://arxiv.org/pdf/1810.08280> 5.<https://www.semanticscholar.org/paper/Adversarial-Example-Attacks-Toward-Android-Malware-Li-Zhou/a87bc35899e998131b59b1b2d4ac78e43a2a1e7f> 6.<https://arxiv.org/abs/2004.11898> 7.[https://github.com/AhsanAyub/adversarial\_ml\_ids](https://github.com/AhsanAyub/adversarial_ml_ids) 8.<https://arxiv.org/html/2312.03245v1> 9.<https://cse.hkust.edu.hk/pg/research/projects/qianzh/iot-sensing/> 10.<https://www.semanticscholar.org/paper/SpacePhish%3A-The-Evasion-space-of-Adversarial-using-Apruzzese-Conti/25d722877d627c05711e81c4bd3dab09c5f08ff1>
发表于 2024-09-23 09:00:02
阅读 ( 5532 )
分类:
其他
0 推荐
收藏
0 条评论
请先
登录
后评论
elwood1916
29 篇文章
×
发送私信
请先
登录
后发送私信
×
举报此文章
垃圾广告信息:
广告、推广、测试等内容
违规内容:
色情、暴力、血腥、敏感信息等内容
不友善内容:
人身攻击、挑衅辱骂、恶意行为
其他原因:
请补充说明
举报原因:
×
如果觉得我的文章对您有用,请随意打赏。你的支持将鼓励我继续创作!