问答
发起
提问
文章
攻防
活动
Toggle navigation
首页
(current)
问答
商城
实战攻防技术
活动
摸鱼办
搜索
登录
注册
从CTF和勒索样本中学习AES加密算法逆向识别
CTF
如何IDA静态识别AES,帮助工作中有个快速定位算法的方法
AES(Advanced Encryption Standard)又称为Rijndael加密法,AES的出现是为了取代DES,因为DES分组相对较小,最终Rijndael算法获选AES。 它满足如下条件: 1、分组大小为128的分组密码。 2、支持三种密码标准:128位、192位和256位。 3、软硬件实现高效。 对于不同的密钥长度,加密方式类似,只是128位循环10次,192位循环12次,256位循环14次。其中明文长度必须事16的倍数,如果不是16的倍数需要对明文数据进行填充后进行加密。这里的位数表示密钥可选的位数,密钥大小和明文数据大小必须是32的倍数。但是运算时被加密的数据块只能被切割成4\*4=16字节的矩阵。 填充模式有以下几种: NONE、PKC37、ZERO、ANSI923、IOS7816\_4、IOS10126 AES中用到了一个S盒(S-BOX),是由加密者提供给被加密数据的一个替换表,用于SubBytes操作中,将每个字节根据码表替换。 AES加密描述 ======= 整个加密过程的语言描述 ```php 明文数据填充 根据密钥进行拓展密钥算法计算轮密钥 初始轮(1) AddRoundKey 第一轮将State(明文矩阵)与第一轮的轮密钥进行异或 中间轮(2~9) SubBytes:将数据块中的数据,映射到 Rijndael S-box,主要为了消除特征 ShiftRows:将数据块按“行”移位,以达到混淆的目的 MixColumns:将数据块按“列”与一个由多项式构成的 matrix,做矩阵乘法。目的是将单个错误扩散到整体,从而达到雪崩效应的预 期,使其更难被破解 AddRoundKey:将本轮的 轮密钥与数据块进行异或 最终轮(10) SubBytes ShiftRows AddRoundKey ``` 图解完整加密流程  使用的轮数和扩展密钥 EK 的大小取决于所提供原始密钥的大小。下表显示了原始密钥长度、循环次数和扩展密钥长度之间的相关性: 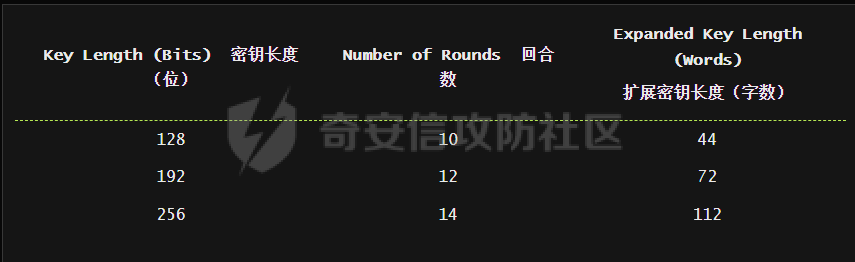 State(状态矩阵) =========== 在分组密码中经常会提到State的概念,其本质就是我们上述的分组明文数据,把明文数据分成多个4\*4的数据块。第一个字节将位于第一列第一行,第二个字节将位于第一列第二行。如下图所示, P 表示明文数组, Px 表示明文数组索引 x 处的字节:  key Expansion(密钥拓展) =================== AES 的扩展密钥是一个由原始密钥派生的四字节字组成的列表。数组中的第一个字与原始密钥相同。例如,密钥数组中的前四个字节就是扩展密钥中的第一个字 EK ,如下所示: ```python key = [0x00, 0x11, 0x22, 0x33, 0x44, 0x55, 0x66, 0x77, 0x88, 0x99, 0xaa, 0xbb, 0xcc, 0xdd, 0xee, 0xff] expanded_key = [0x00112233, 0x44556677, 0x8899aabb, 0xccddeeff, ...] ``` 每个附加字都是前一个字与索引 i - NK 处的字进行 XOR 的结果,其中 i 是当前索引, NK 是原始密码密钥字的数量(一个字占4字节,4字/128位、6字/192位 或 8字/256位,取决于密钥的位数)。当当前索引是 NK 的倍数时,前一个字会在进行 XOR 之前被转换。这包括将字向左旋转一个(即 0xAABBCCDD 变为 0xBBCCDDAA ),然后将每个字节替换为 AES 的替换盒(S-Box)--一个 256 字节数组--中的一个值。然后,新的四字节字与 "循环常数" RCON 进行 XOR。舍入常数 RCON 可以通过算法计算得出(该数学公式不做过深讨论):。对于标准 AES-128 算法,还可以使用以下值对轮常量进行硬编码:  整个 AES-128 密钥扩展算法看起来就像下面的 Python 代码: ```php # Round Constants # 定义的轮常量用于编码拓展密钥,标准AES-128可以将下列值转换为字单位数据与拓展密钥转换的字数据进行异或 RCON = [None, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1B, 0x36] # 该函数用于将输入的数据流转换成多个字数组,用于后续与轮常量进行异或 # AES中,该输入为拓展密钥(EK),将拓展密钥从字节流转换成字数组形式并于S-Box进行替换 def subword(self, word): """AES SubWord Method. Args: word (list): Word to transform Returns: int: Transformed word """ bs = struct.pack('>I', word) nw = [] for b in bs: nw.append(self.s_box[b]) nw = struct.unpack('>I', bytes(nw))[0] return nw # 该函数用于 def rotword(self, word): """AES RotateWord Method. Args: word (list): Word to transform Returns: int: Transformed word """ bs = list(struct.pack('>I', word)) bs.append(bs.pop(0)) nw = struct.unpack('>I', bytes(bs))[0] return nw # 根据轮常量生成拓展密钥 def key_expansion(self, key): """AES Key Expansion Algorithm. Args: key (bytes): Key to expand Returns: list: List of words for expanded key """ ek = [] i = 0 # 把原始密钥保存到拓展密钥开头,128位保存4个字,192保存6个字,256保存8个字,循环分别对应4、6、8 while i < 4: b = bytes(key[i*4:(i*4)+4]) w = struct.unpack('>I', b)[0] ek.append(w) i += 1 # 根据密钥长度生成拓展密钥EK,如128生成44个字的拓展密钥数组,192生成72个字数组,256生成112个字数组 while i < 44: # 将上一个运算结果存储到tmp用于后续运算,因为前面的4轮所以进入该循环时i=4 tmp = ek[i-1] # 这里nk = 4,因为AES-128原始密钥长度只能生成4个字。 if i % 4 == 0: # 把轮常量转换成字数组,用于与拓展密钥数据进行异或。不足的地方补0 rcon_val = struct.unpack('>I', bytes([self.RCON[i//4], 0, 0, 0]))[0] # 按照编码流程对拓展密钥进行编码运算 tmp = self.subword(self.rotword(tmp)) ^ rcon_val # 将tmp生成的值按照上面描述的运算方法进行异或生成最终的拓展密钥字 nw = tmp ^ ek[i-4] ek.append(nw) i += 1 return ek ``` AddRoundKey(轮密钥加) ================= 本质上就是将数据矩阵与密钥矩阵进行逐个字节异或。下图所示P为明文数据,K为密钥矩阵。将32倍数的明文分割成多个4\*4=16字节的矩阵,用于轮密钥加运算。 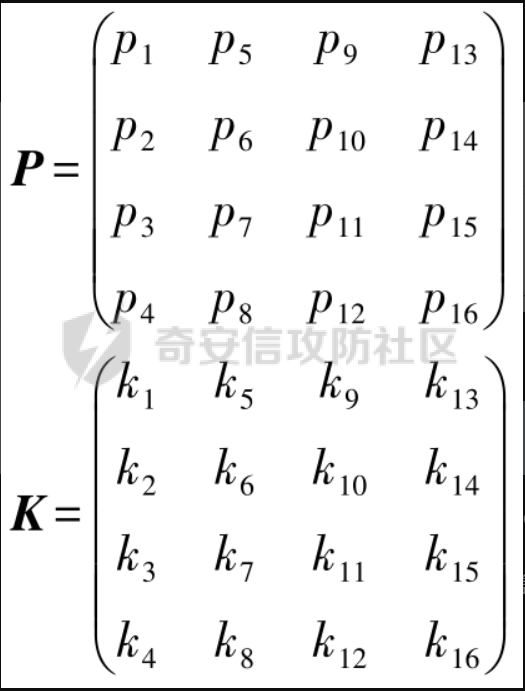 数据层面转换如下 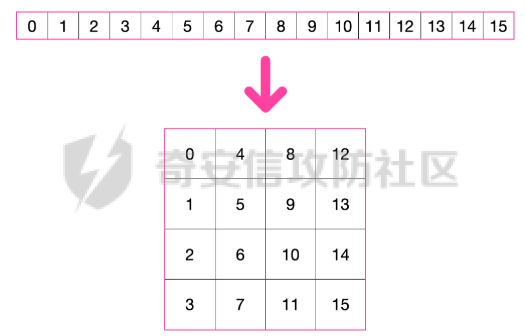 AES 之所以保证安全的关键,是对每个数据块执行多轮加密,对于 128 bits 的密钥块,至少需要 6+128/32=10 轮。 这里除数 32 是由于 Rijndael 的数据块、密钥块大小必须是 32 的倍数,最小 128,最大 256,只是 AES 仅选择了其中的 128、192、256 三组作为密钥块大小,数据块则固定为 128。 进行轮密钥加就是对矩阵中每个元素一一对应进行异或  代码实现 ```js def add_round_key(s,k): for i in range(4): for j in range(4): s_box[i][j] ^= k[i][j] ``` SubByte(字节替换) ============= 在这里,引入一个S盒(S-box),也就是一个替换表,如下。 按照数学逻辑的二维矩阵数学逻辑替换 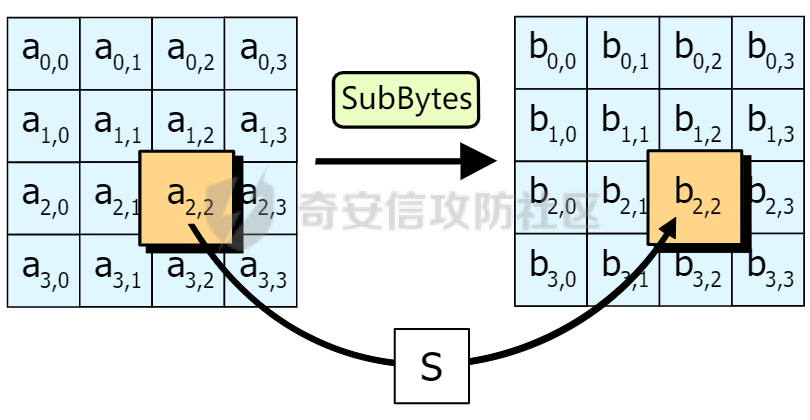 代码层面可以按照1维数组的逻辑图  加密的时候使用的是S-BOX,解密的时候也有一个与其对应的S-BOX表。AES给出的现成加解密S-BOX分别如下。s\_box用于加密,s\_box\_inv用于解密。 ```js s_box = [ [0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76], [0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0], [0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15], [0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75], [0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84], [0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf], [0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8], [0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2], [0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73], [0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb], [0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79], [0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08], [0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a], [0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e], [0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf], [0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16] ] s_box_inv = [ [0x52, 0x09, 0x6a, 0xd5, 0x30, 0x36, 0xa5, 0x38, 0xbf, 0x40, 0xa3, 0x9e, 0x81, 0xf3, 0xd7, 0xfb], [0x7c, 0xe3, 0x39, 0x82, 0x9b, 0x2f, 0xff, 0x87, 0x34, 0x8e, 0x43, 0x44, 0xc4, 0xde, 0xe9, 0xcb], [0x54, 0x7b, 0x94, 0x32, 0xa6, 0xc2, 0x23, 0x3d, 0xee, 0x4c, 0x95, 0x0b, 0x42, 0xfa, 0xc3, 0x4e], [0x08, 0x2e, 0xa1, 0x66, 0x28, 0xd9, 0x24, 0xb2, 0x76, 0x5b, 0xa2, 0x49, 0x6d, 0x8b, 0xd1, 0x25], [0x72, 0xf8, 0xf6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xd4, 0xa4, 0x5c, 0xcc, 0x5d, 0x65, 0xb6, 0x92], [0x6c, 0x70, 0x48, 0x50, 0xfd, 0xed, 0xb9, 0xda, 0x5e, 0x15, 0x46, 0x57, 0xa7, 0x8d, 0x9d, 0x84], [0x90, 0xd8, 0xab, 0x00, 0x8c, 0xbc, 0xd3, 0x0a, 0xf7, 0xe4, 0x58, 0x05, 0xb8, 0xb3, 0x45, 0x06], [0xd0, 0x2c, 0x1e, 0x8f, 0xca, 0x3f, 0x0f, 0x02, 0xc1, 0xaf, 0xbd, 0x03, 0x01, 0x13, 0x8a, 0x6b], [0x3a, 0x91, 0x11, 0x41, 0x4f, 0x67, 0xdc, 0xea, 0x97, 0xf2, 0xcf, 0xce, 0xf0, 0xb4, 0xe6, 0x73], [0x96, 0xac, 0x74, 0x22, 0xe7, 0xad, 0x35, 0x85, 0xe2, 0xf9, 0x37, 0xe8, 0x1c, 0x75, 0xdf, 0x6e], [0x47, 0xf1, 0x1a, 0x71, 0x1d, 0x29, 0xc5, 0x89, 0x6f, 0xb7, 0x62, 0x0e, 0xaa, 0x18, 0xbe, 0x1b], [0xfc, 0x56, 0x3e, 0x4b, 0xc6, 0xd2, 0x79, 0x20, 0x9a, 0xdb, 0xc0, 0xfe, 0x78, 0xcd, 0x5a, 0xf4], [0x1f, 0xdd, 0xa8, 0x33, 0x88, 0x07, 0xc7, 0x31, 0xb1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xec, 0x5f], [0x60, 0x51, 0x7f, 0xa9, 0x19, 0xb5, 0x4a, 0x0d, 0x2d, 0xe5, 0x7a, 0x9f, 0x93, 0xc9, 0x9c, 0xef], [0xa0, 0xe0, 0x3b, 0x4d, 0xae, 0x2a, 0xf5, 0xb0, 0xc8, 0xeb, 0xbb, 0x3c, 0x83, 0x53, 0x99, 0x61], [0x17, 0x2b, 0x04, 0x7e, 0xba, 0x77, 0xd6, 0x26, 0xe1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0c, 0x7d] ] ``` 替换方式如下 ```js # 二位矩阵的替换逻辑 def sub_bytes(s): for i in range(4): s[i][j] = s_box[s[i][j]] # 也可以写成一维数组的替换逻辑 def sub_bytes(self, state): """AES SubBytes Method. Args: state (list): AES State """ for i in range(len(state)): state[i] = self.s_box[state[i]] ``` ShiftRows(行置换) ============== 这也是一次扩散处理,达到雪崩效应。第一行不变,第二行左移1,第三行左移2,第四行左移3,即矩阵P变成  具体如下 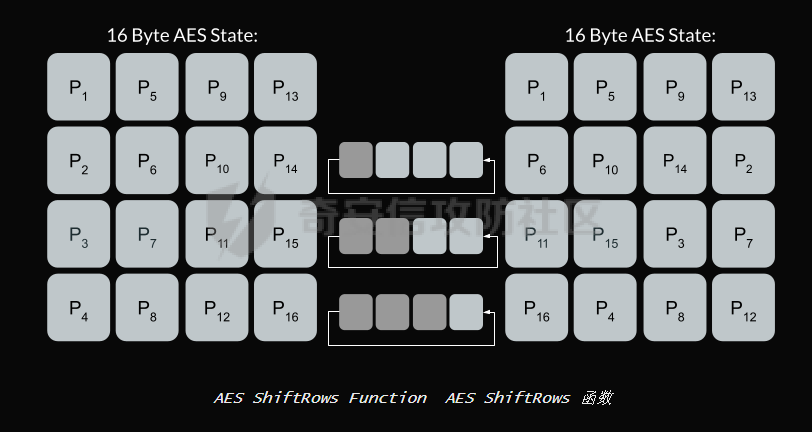 代码如下 ```js # 二维矩阵的左移(带解密) def shift_rows(grid, inv=False): for i in range(4): if inv: # for decryption grid[i::4] = grid[i::4][-i:] + grid[i::4][:-i] else: grid[i::4] = grid[i::4][i:] + grid[i::4][:i] # 一维数组的替换逻辑(只有加密) def shift_rows(self, state): """AES ShiftRows Method. Args: state (list): AES State """ for i in range(1, 4): state[i*4:(i*4)+4] = state[(i*4)+i:(i*4)+4] + state[(i*4):(i*4)+i] ``` MixColumn(列混淆) ============== 同样也是扩散操作,将给定矩阵和P在GF(2^8)有限域做乘法。 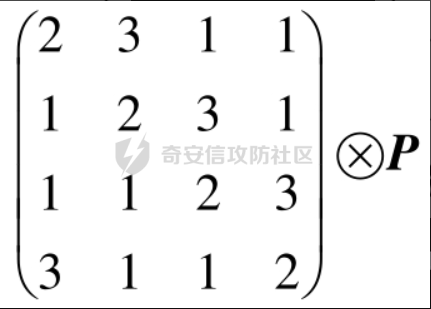 就是将进行完前三轮的数据P与最小优先域做矩阵乘法 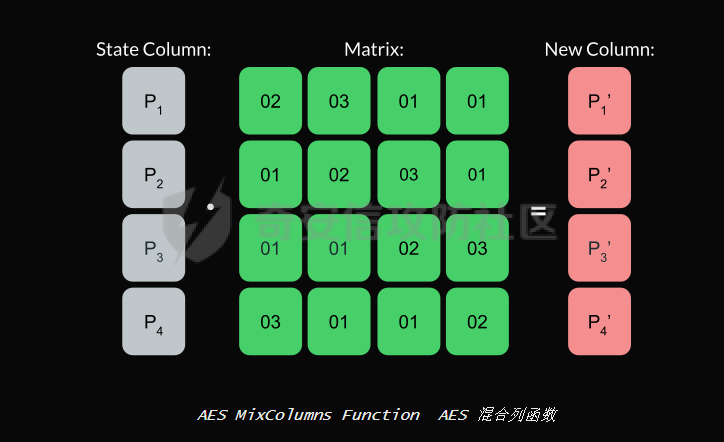 用作运算的矩阵可在 [Rijndael MixColumns](https://en.wikipedia.org/wiki/Rijndael_MixColumns#InverseMixColumns) 中找到,大概长这样: 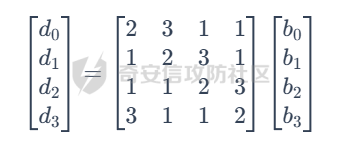 用于解密的矩阵:  具体可以参考[https://sxyz.blog/aes-from-scratch](https://sxyz.blog/aes-from-scratch/) 这一步需要复杂的公式推导,具体可以参考上面的参考链接。在逆向过程中可以不拿此步作为特征识别 ```js # 二维矩阵的替换逻辑 def mix_columns(grid): def mul_by_2(n): s = (n << 1) & 0xff if n & 128: s ^= 0x1b return s def mul_by_3(n): return n ^ mul_by_2(n) def mix_column(c): return [ mul_by_2(c[0]) ^ mul_by_3(c[1]) ^ c[2] ^ c[3], # [2 3 1 1] c[0] ^ mul_by_2(c[1]) ^ mul_by_3(c[2]) ^ c[3], # [1 2 3 1] c[0] ^ c[1] ^ mul_by_2(c[2]) ^ mul_by_3(c[3]), # [1 1 2 3] mul_by_3(c[0]) ^ c[1] ^ c[2] ^ mul_by_2(c[3]), # [3 1 1 2] ] for i in range(0, 16, 4): grid[i:i + 4] = mix_column(grid[i:i + 4]) # 一维数组的替换逻辑 def gmul(a, b): """Special AES function used for multiplication Args: a (int): Integer to multiply b (int): Integer to multiply Returns: int: The product of the values """ p = 0 for c in range(8): if b & 1: p ^= a a <<= 1 if a & 0x100: a ^= 0x11b b >>= 1 return p def mix_columns(self, state): """AES MixColumns Method. Args: state (list): AES State """ for i in range(4): a = state[i] # 第一列 b = state[i+4] # 第二列 c = state[i+8] # 第三列 d = state[i+12] # 第四列 state[i] = gmul(2, a) ^ gmul(3, b) ^ c ^ d # [2 3 1 1] state[i+4] = a ^ gmul(2, b) ^ gmul(3, c) ^ d # [1 2 3 1] state[i+8] = a ^ b ^ gmul(2, c) ^ gmul(3, d) # [1 1 2 3] state[i+12] = gmul(3, a) ^ b ^ c ^ gmul(2, d) # [3 1 1 2] ``` 逆向实战 ==== 强网拟态2024babyre -------------- 下载地址 <https://xzfile.aliyuncs.com/upload/affix/20241106132915-0ff3ee08-9c00-1.zip> 使用IDA打开如图 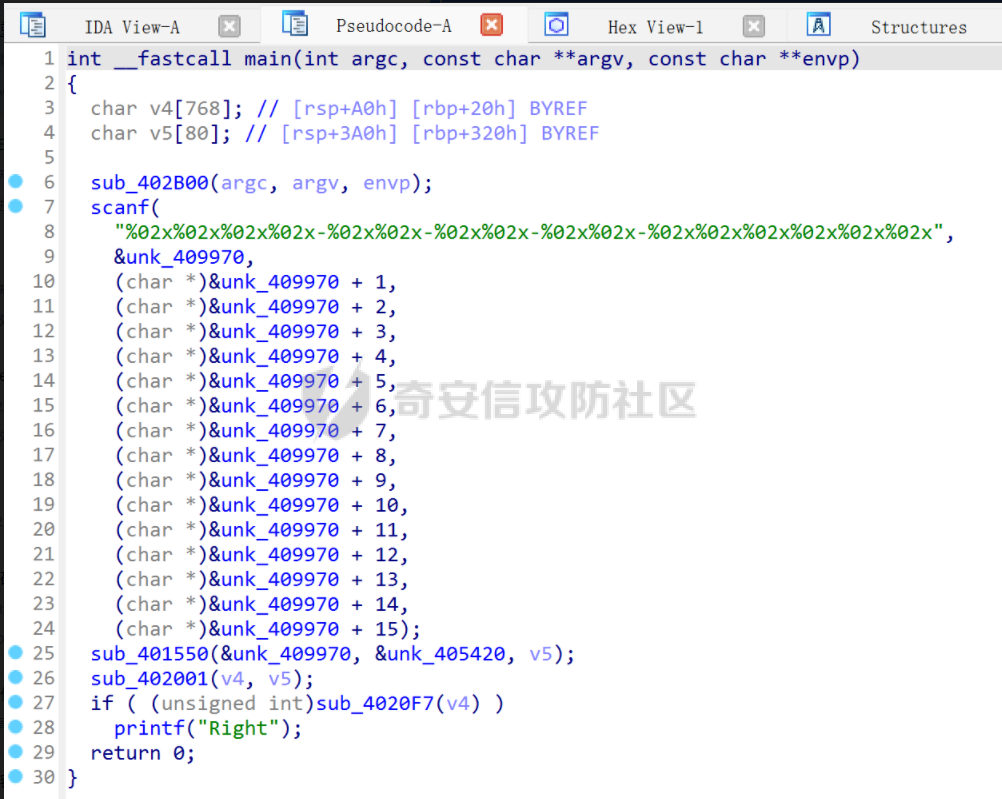 调整后如下数据类型为字节数组后,可以看到大概逻辑就是讲flag传入sub\_401550进行解密 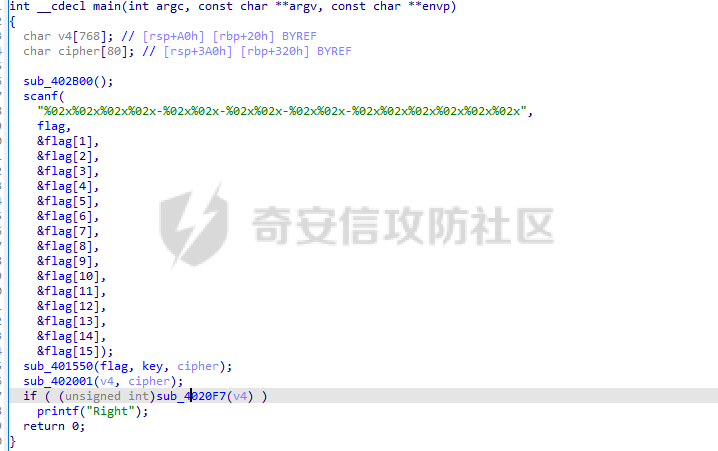 进入sub\_401550,可以看到sub\_401bce被调用了3次,根据上面列出的加密顺序合理猜测为AddRoundKey操作 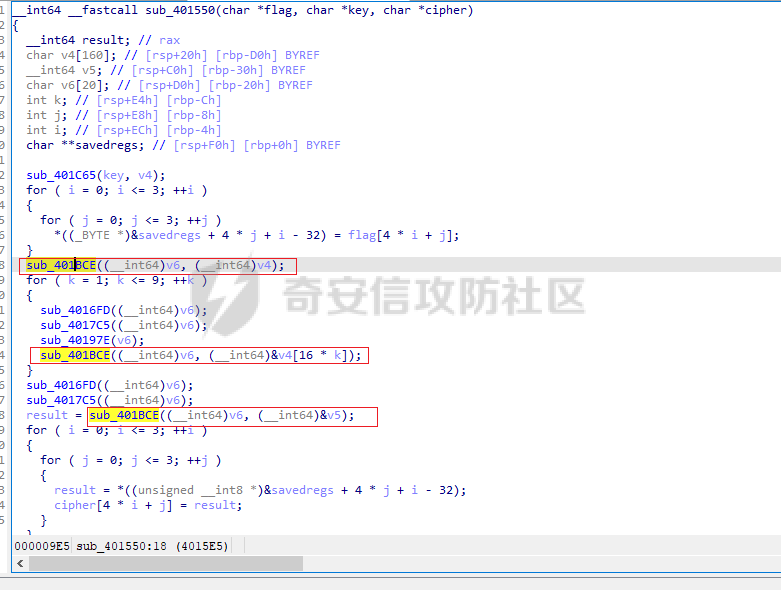 根据加密轮的顺序合理猜测调整如下  可以看到就是简单的p和key矩阵逐个字节异或。为4\*4的矩阵与AES-128的key一致  查看字节替换 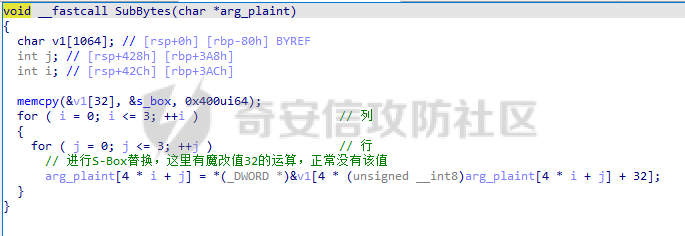 双击进入s\_box全局变量,可以看到作者鸡贼的把S-box写成了4字节间隔,这样常见的密码扫描工具就扫不出来了  左移矩阵  最后简单看下列混淆即可,逆向过程中大概有个概念就行  我们重新回到AES加密函数,查看第一个函数,也就是密钥拓展函数中,也就是加密轮开始之前的函数。  进入key\_extend函数可以看到函数sub\_401ec2  进入该函数可以看到前文描述的轮常量和S-Box的替换算法  google下常量值可以定位到AES源码,本质就是对应对应的字节  ```js 0x1000000,0x2000000,0x4000000,0x8000000,0x10000000,0x20000000,0x40000000,0x80000000,0x1B000000,0x36000000 ``` [https://github.com/openssl/openssl/blob/master/crypto/aes/aes\_core.c](https://github.com/openssl/openssl/blob/master/crypto/aes/aes_core.c) 可以发现是OpenSSL在对AES-128加密时产生的轮常量,再次验证了该加密算法为AES-128 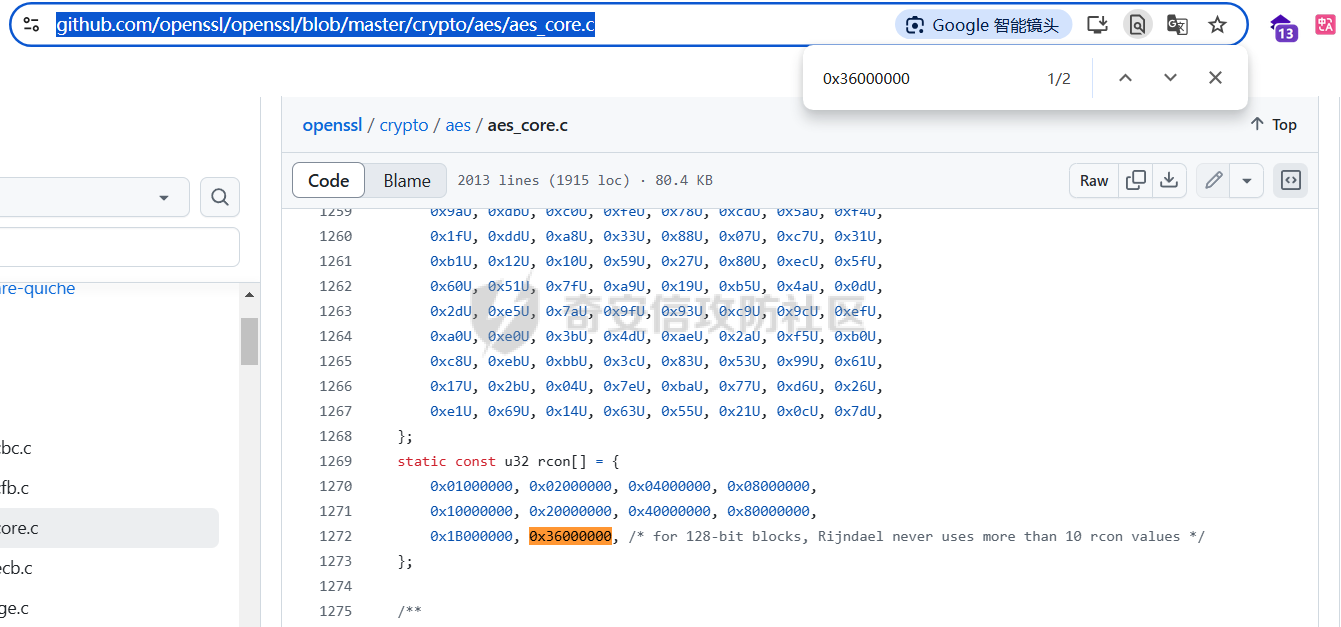 AES T表(T-Table)查找方法(AES查表优化) ============================ 为了提高 AES 算法的效率,MixColumns、ShiftRows 和 SubBytes 函数被合并优化为一个操作,使用五个查找表。密钥扩展算法与原始 AES 算法相同,State被视为普通数组,而不是 4x4 矩阵。 说人话就是为了减少轮中的计算次数,人们根据公式简化了AES加密的步骤。我们可以观察下图。正常的加密一轮是如下顺序  但是SubByte和ShiftRows是可以交换顺序的——即先做字节代换层再做ShiftRows层和先做ShiftRows层再做字节代换层的结果是完全一样的。如果将它们交换,那么ShiftRows层实际上就是按照特定的顺序去读取这一轮操作的输入数据。字节代换层和MixColumn层融合为查找表。轮密钥加[按位异或](https://zhida.zhihu.com/search?content_id=8454173&content_type=Article&match_order=1&q=%E6%8C%89%E4%BD%8D%E5%BC%82%E6%88%96&zhida_source=entity),这个操作很简单,直接附在后面就行就相当于矩阵加法。 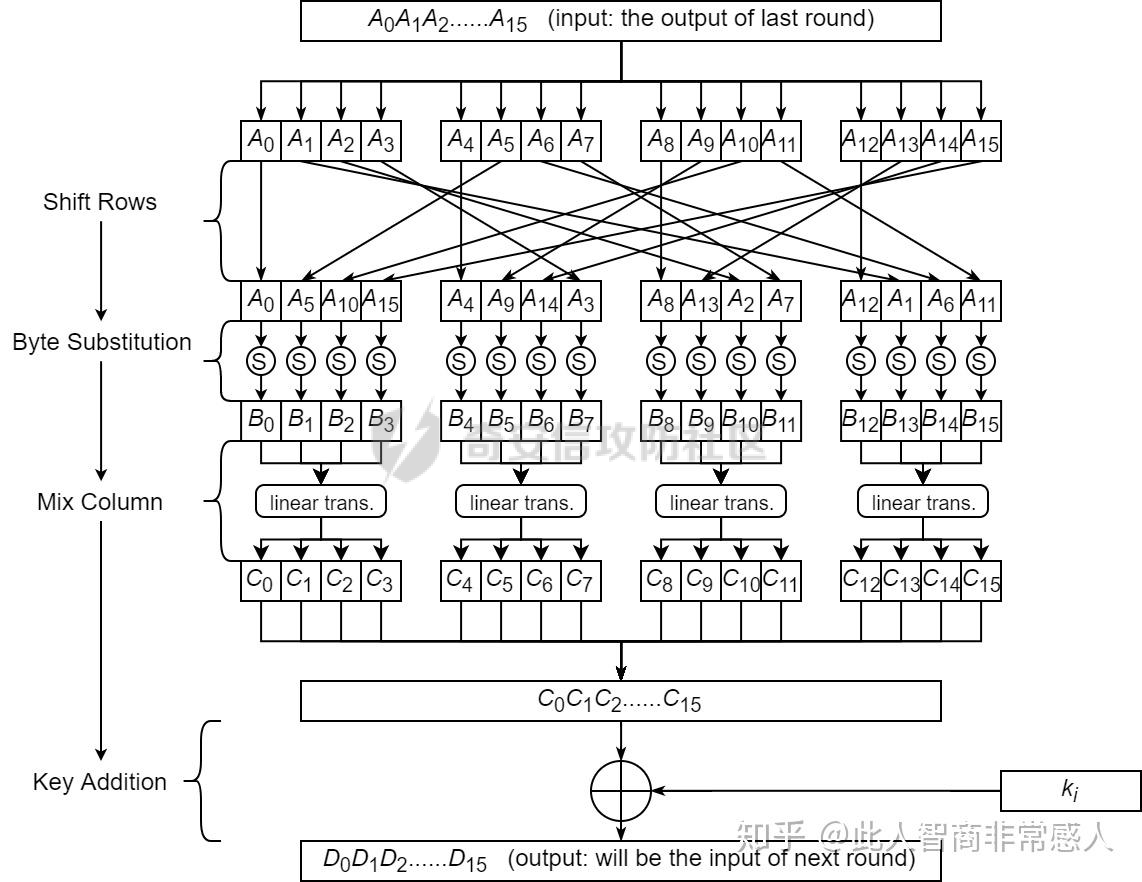 这样的化前三个操作都是符合数学中的矩阵变化,Shift Rows就是平移矩阵的行、SubByte就是根据S-Box按字节替换,而且标准AES的S-BOX是固定的所以最初的状态值也相当于已知。又因为列混淆就是矩阵乘法运算,所以将三个公式可以提前运算出下图的矩阵等式。注意,C矩阵是前三个操作的结果,此时还没有进行最后的轮密钥加  可以根据矩阵继续提取出新的等式  其中B是S-Box替换操作,所以可以继续分解成S(A),这里A是未加密的明文矩阵块拆成的列。有了前三个矩阵操作步骤,最后一步就是加上对应的轮密钥即可。也就是下图的Wk0。  我们将T盒(T-Box)作如下定义,即可基于前面两篇文章的知识,通过编写程序算法计算出四个Te表(T表):  最后1-9/11/13轮之间,每轮的操作就变成了以下公式。开发者只需要提前算出T表就可以大大节省操作,使AES被简化。计算机中通常将每一个列向量看作一个整体,储存为一个32位无符号整数(Int32),因此每一个T表都是一个有2^8=256个Int32组成的数组。  T表(T-Table)生成器 -------------- 每次从S-Box读一个字节,然后根据S-Box的单字节为每个T-Tables生成一个字,一循环256次为每个T-Tables生成256个字 ```js T1 = {s_box[i] * 2, s_box[i], s_box[i], s_box[i] * 3} # [2,1,1,3] T2 = {s_box[i] * 3, s_box[i] * 2, s_box[i], s_box[i]} # [3,2,1,1] T3 = {s_box[i], s_box[i] * 3, s_box[i] * 2, s_box[i]} # [1,3,2,1] T4 = {s_box[i], s_box[i], s_box[i] * 3, s_box[i] * 2} # [1,1,3,2] ``` 对应数学概念  最后的 T 表将 S-Box 的每个字节组合成一个四字节字,只在最后一轮加密时使用。 ```js # Final T-Table generation T5 = {s_box[i], s_box[i], s_box[i], s_box[i]} ``` 整个查找表的生成器的 Python 代码 ```js # 一维数组对应的矩阵乘法逻辑 def gmul(a, b): """Special AES function used for multiplication Args: a (int): Integer to multiply b (int): Integer to multiply Returns: int: The product of the values """ p = 0 for c in range(8): if b & 1: p ^= a a <<= 1 if a & 0x100: a ^= 0x11b b >>= 1 return p def generate_t_tables(self): """Generates the tables used for the AES lookup table method.""" self.t1 = [] self.t2 = [] self.t3 = [] self.t4 = [] self.t5 = [] #每次循环计算相当于对矩阵的列进行T表合并计算 for i in range(len(self.s_box)): # 根据S-Box的第一个字节计算出5个T表的字 word1 = [gmul(self.s_box[i], 2), self.s_box[i], self.s_box[i], gmul(self.s_box[i], 3)] word2 = [gmul(self.s_box[i], 3), gmul(self.s_box[i], 2), self.s_box[i], self.s_box[i]] word3 = [self.s_box[i], gmul(self.s_box[i], 3), gmul(self.s_box[i], 2), self.s_box[i]] word4 = [self.s_box[i], self.s_box[i], gmul(self.s_box[i], 3), gmul(self.s_box[i], 2)] word5 = [self.s_box[i]] * 4 self.t1.append(struct.unpack('>I', bytes(word1))[0]) self.t2.append(struct.unpack('>I', bytes(word2))[0]) self.t3.append(struct.unpack('>I', bytes(word3))[0]) self.t4.append(struct.unpack('>I', bytes(word4))[0]) self.t5.append(struct.unpack('>I', bytes(word5))[0]) ``` 基于T-Tables的轮密钥加 --------------- 在每一轮加密中,AES T 表算法将对原始明文数组索引处的四个查找表中的一个字节进行 XOR。例如,一轮普通加密的伪代码如下: ```js # 根据state矩阵生成第一轮轮密钥 around_key[0] = plaint[0:4] ^ ek[0] around_key[1] = plaint[4:8] ^ ek[1] around_key[2] = plaint[8:12] ^ ek[2] around_key[3] = plaint[12:16] ^ ek[3] # AES-128的nk为4固定值 nk = 4 for round in NUM_ROUNDS: # 每一轮都生成around_key,覆盖S-Box的前16位 s_box[0:4] = around_key[0] # Convert word to bytes s_box[4:8] = around_key[1] s_box[8:12] = around_key[2] s_box[12:16] = around_key[3] # 优化后的轮密钥加 around_key[0] = T1[s_box[0]] ^ T2[s_box[5]] ^ T3[s_box[10]] ^ T4[s_box[15]] ^ ek[nk+0] around_key[1] = T1[s_box[4]] ^ T2[s_box[9]] ^ T3[s_box[14]] ^ T4[s_box[3]] ^ ek[nk+1] around_key[2] = T1[s_box[8]] ^ T2[s_box[13]] ^ T3[s_box[2]] ^ T4[s_box[7]] ^ ek[nk+2] around_key[3] = T1[s_box[12]] ^ T2[s_box[1]] ^ T3[s_box[6]] ^ T4[s_box[11]] ^ ek[nk+3] ``` 最后一步轮密钥加操作 ---------- 最后一轮加密与普通加密类似,但它使用的是第五个 T 表,每个 XOR 都会附加到密文中。下面的伪代码演示了这一过程: ```js CT[0:4] = T5[s_box[0]] ^ T5[s_box[5]] ^ T5[s_box[10]] ^ T5[s_box[15]] ^ ek[nk+0] CT[4:8] = T5[s_box[4]] ^ T5[s_box[9]] ^ T5[s_box[14]] ^ T5[s_box[3]] ^ ek[nk+1] CT[8:12] = T5[s_box[8]] ^ T5[s_box[13]] ^ T5[s_box[2]] ^ T5[s_box[7]] ^ ek[nk+2] CT[12:16] = T5[s_box[12]] ^ T5[s_box[1]] ^ T5[s_box[6]] ^ T5s_box[11]] ^ ek[nk+3] ``` AES T表优化后的加密算法 -------------- 而C语言可以参考以下链接 <https://android.googlesource.com/platform/external/openssh/+/idea133/rijndael.c> ```js def cipher_t_table(self, pt): """Lookup Table AES implementation. Args: pt (bytes): Plaintext to encrypt Returns: bytes: Encrypted Ciphertext """ ct = [] around_key = [0, 0, 0, 0] tmp = [0, 0, 0, 0] # 根据拓展密钥初始化轮密钥 around_key[0] = struct.unpack('>I', plaint[0:4])[0] ^ self.ek[0] around_key[1] = struct.unpack('>I', plaint[4:8])[0] ^ self.ek[1] around_key[2] = struct.unpack('>I', plaint[8:12])[0] ^ self.ek[2] around_key[3] = struct.unpack('>I', plaint[12:16])[0] ^ self.ek[3] print(a) # 前9轮加密 for round in range(1, 10): # 每一轮进行4字节转换成一个字 for i in range(4): # 通过字节位移运算每个字,并生成新的轮密钥 tmp[i] = (self.t1[(around_key[i]; 24) & 0xff] ^ self.t2[(around_key[(i + 1) % 4] >> 16) & 0xff] ^ self.t3[(around_key[(i + 2) % 4] >> 8) & 0xff] ^ self.t4[(around_key[(i + 3) % 4]) & 0xff] ^ self.ek[(round*4)+i]) around_key = tmp.copy() # 最后一轮加密 for i in range(4): ct.append(self.s_box[(a[i] >> 24) & 0xff] ^ ((self.ek[-4+i] >> 24) & 0xff)) ct.append(self.s_box[(a[(i + 1) % 4] >> 16) & 0xff] ^ ((self.ek[-4+i] >> 16) & 0xff)) ct.append(self.s_box[(a[(i + 2) % 4] >> 8) & 0xff] ^ ((self.ek[-4+i] >> 8) & 0xff)) ct.append(self.s_box[(a[(i + 3) % 4]) & 0xff] ^ ((self.ek[-4+i]) & 0xff)) return bytes(ct) ``` 以Sodinokibi勒索软件为例 ----------------- 样本下载地址 <https://app.any.run/tasks/41cee64f-b909-4eaf-a106-16865999db4f/> 因为我们知道AES优化的T表是根据S-Box逐个字节运算得来,所以我们可以手动计算T表的前4字节。因为只有前4字节使用的是ek\[nk+0\]不受ek影响 ```js [0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76] ``` 计算结果如下 ```js t0 = [0xc66363a5] t1 = [0xa5c66363] t2 = [0x63a5c663] t3 = [0x6363a5c6] ``` ida搜索字节顺序搜索 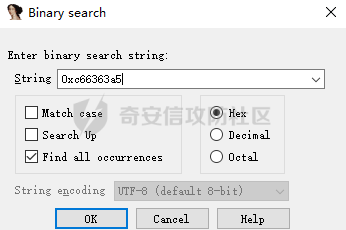 可以搜到对应T0 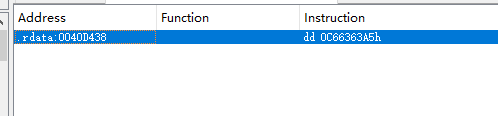 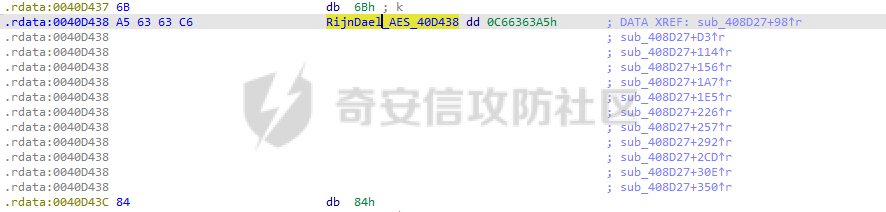 交叉引用可以来到轮密钥加  同理我们可以定位t1、t2、t3  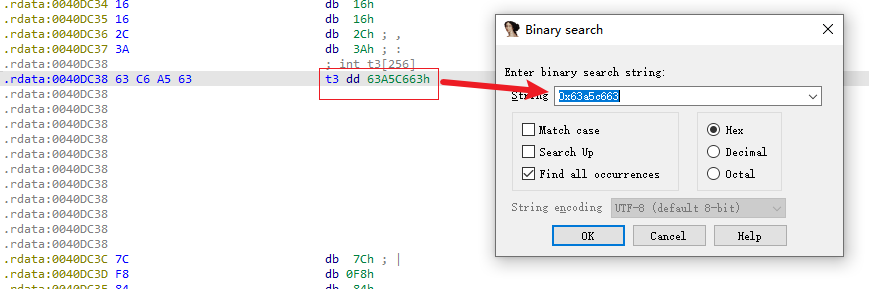 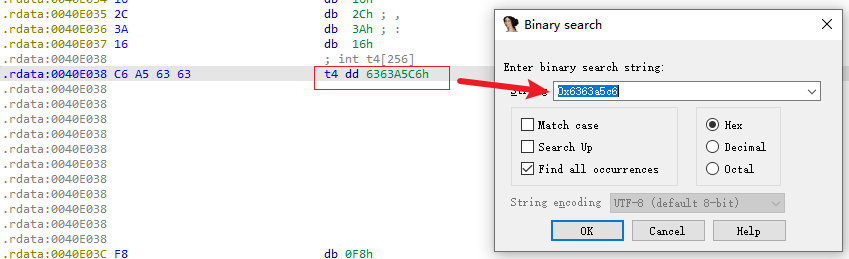 由于不影响AES的ek生成,所以rcon的也不变,也可搜索到对应特征,但是该rcon被嵌入在其他数据中无交叉引用所以无法直接用来定位加密算法 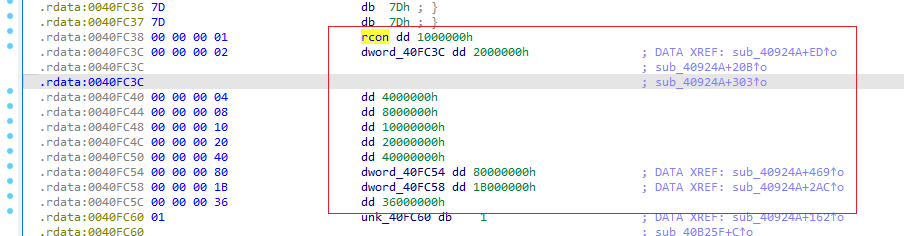 还可以根据基数轮与偶数轮再次进行优化,这样算法需要遍历的次数更少速度就更快 ```js let mut wa0: u32 = ((input[ 0] as u32) << 24) ^ ((input[ 1] as u32) << 16) ^ ((input[ 2] as u32) << 8) ^ (input[ 3] as u32) ^ keys[0]; let mut wa1: u32 = ((input[ 4] as u32) << 24) ^ ((input[ 5] as u32) << 16) ^ ((input[ 6] as u32) << 8) ^ (input[ 7] as u32) ^ keys[1]; let mut wa2: u32 = ((input[ 8] as u32) << 24) ^ ((input[ 9] as u32) << 16) ^ ((input[10] as u32) << 8) ^ (input[11] as u32) ^ keys[2]; let mut wa3: u32 = ((input[12] as u32) << 24) ^ ((input[13] as u32) << 16) ^ ((input[14] as u32) << 8) ^ (input[15] as u32) ^ keys[3]; // round 1 let mut wb0: u32 = TE0[ (wa0 >> 24) as usize ] ^ TE1[((wa1 >> 16) as usize) & 0xFF] ^ TE2[((wa2 >> 8) as usize) & 0xFF] ^ TE3[( wa3 as usize) & 0xFF] ^ keys[4]; let mut wb1: u32 = TE0[ (wa1 >> 24) as usize ] ^ TE1[((wa2 >> 16) as usize) & 0xFF] ^ TE2[((wa3 >> 8) as usize) & 0xFF] ^ TE3[( wa0 as usize) & 0xFF] ^ keys[5]; let mut wb2: u32 = TE0[ (wa2 >> 24) as usize ] ^ TE1[((wa3 >> 16) as usize) & 0xFF] ^ TE2[((wa0 >> 8) as usize) & 0xFF] ^ TE3[( wa1 as usize) & 0xFF] ^ keys[6]; let mut wb3: u32 = TE0[ (wa3 >> 24) as usize ] ^ TE1[((wa0 >> 16) as usize) & 0xFF] ^ TE2[((wa1 >> 8) as usize) & 0xFF] ^ TE3[( wa2 as usize) & 0xFF] ^ keys[7]; // round 2 to round 9 (or 11, 13) for i in 1..(rounds / 2) { // even-number rounds wa0 = TE0[ (wb0 >> 24) as usize ] ^ TE1[((wb1 >> 16) as usize) & 0xFF] ^ TE2[((wb2 >> 8) as usize) & 0xFF] ^ TE3[( wb3 as usize) & 0xFF] ^ keys[8 * i]; wa1 = TE0[ (wb1 >> 24) as usize ] ^ TE1[((wb2 >> 16) as usize) & 0xFF] ^ TE2[((wb3 >> 8) as usize) & 0xFF] ^ TE3[( wb0 as usize) & 0xFF] ^ keys[8 * i + 1]; wa2 = TE0[ (wb2 >> 24) as usize ] ^ TE1[((wb3 >> 16) as usize) & 0xFF] ^ TE2[((wb0 >> 8) as usize) & 0xFF] ^ TE3[( wb1 as usize) & 0xFF] ^ keys[8 * i + 2]; wa3 = TE0[ (wb3 >> 24) as usize ] ^ TE1[((wb0 >> 16) as usize) & 0xFF] ^ TE2[((wb1 >> 8) as usize) & 0xFF] ^ TE3[( wb2 as usize) & 0xFF] ^ keys[8 * i + 3]; // odd-number rounds wb0 = TE0[ (wa0 >> 24) as usize ] ^ TE1[((wa1 >> 16) as usize) & 0xFF] ^ TE2[((wa2 >> 8) as usize) & 0xFF] ^ TE3[( wa3 as usize) & 0xFF] ^ keys[8 * i + 4]; wb1 = TE0[ (wa1 >> 24) as usize ] ^ TE1[((wa2 >> 16) as usize) & 0xFF] ^ TE2[((wa3 >> 8) as usize) & 0xFF] ^ TE3[( wa0 as usize) & 0xFF] ^ keys[8 * i + 5]; wb2 = TE0[ (wa2 >> 24) as usize ] ^ TE1[((wa3 >> 16) as usize) & 0xFF] ^ TE2[((wa0 >> 8) as usize) & 0xFF] ^ TE3[( wa1 as usize) & 0xFF] ^ keys[8 * i + 6]; wb3 = TE0[ (wa3 >> 24) as usize ] ^ TE1[((wa0 >> 16) as usize) & 0xFF] ^ TE2[((wa1 >> 8) as usize) & 0xFF] ^ TE3[( wa2 as usize) & 0xFF] ^ keys[8 * i + 7]; } // final round output[ 0] = SBOX[ (wb0 >> 24) as usize ] ^ ((keys[keys.len() - 4] >> 24) as u8); output[ 1] = SBOX[((wb1 >> 16) as usize) & 0xFF] ^ ((keys[keys.len() - 4] >> 16) as u8); output[ 2] = SBOX[((wb2 >> 8) as usize) & 0xFF] ^ ((keys[keys.len() - 4] >> 8) as u8); output[ 3] = SBOX[( wb3 as usize) & 0xFF] ^ ( keys[keys.len() - 4] as u8); output[ 4] = SBOX[ (wb1 >> 24) as usize ] ^ ((keys[keys.len() - 3] >> 24) as u8); output[ 5] = SBOX[((wb2 >> 16) as usize) & 0xFF] ^ ((keys[keys.len() - 3] >> 16) as u8); output[ 6] = SBOX[((wb3 >> 8) as usize) & 0xFF] ^ ((keys[keys.len() - 3] >> 8) as u8); output[ 7] = SBOX[( wb0 as usize) & 0xFF] ^ ( keys[keys.len() - 3] as u8); output[ 8] = SBOX[ (wb2 >> 24) as usize ] ^ ((keys[keys.len() - 2] >> 24) as u8); output[ 9] = SBOX[((wb3 >> 16) as usize) & 0xFF] ^ ((keys[keys.len() - 2] >> 16) as u8); output[10] = SBOX[((wb0 >> 8) as usize) & 0xFF] ^ ((keys[keys.len() - 2] >> 8) as u8); output[11] = SBOX[( wb1 as usize) & 0xFF] ^ ( keys[keys.len() - 2] as u8); output[12] = SBOX[ (wb3 >> 24) as usize ] ^ ((keys[keys.len() - 1] >> 24) as u8); output[13] = SBOX[((wb0 >> 16) as usize) & 0xFF] ^ ((keys[keys.len() - 1] >> 16) as u8); output[14] = SBOX[((wb1 >> 8) as usize) & 0xFF] ^ ((keys[keys.len() - 1] >> 8) as u8); output[15] = SBOX[( wb2 as usize) & 0xFF] ^ ( keys[keys.len() - 1] as u8); ``` 经过代码整理可以看到最后识别的加密算法如下,可以看到加密的数据成为下一轮的输入,所以加密模式优先排除ECB加密。AES位数会根据传入的参数进行运算,由此判断是AES-128、AES-192还是AES-256。剩下加密模式需要根据传入参数和状态矩阵是否作为输入进行综合判断。  参考链接 ==== <https://bbs.kanxue.com/thread-90722.htm> <https://zhuanlan.zhihu.com/p/41716899> <https://zhuanlan.zhihu.com/p/41716899> <https://zhuanlan.zhihu.com/p/42264499> <https://goggleheadedhacker.com/blog/post/reversing-crypto-functions-aes>
发表于 2025-02-13 09:00:00
阅读 ( 5658 )
分类:
二进制
1 推荐
收藏
0 条评论
请先
登录
后评论
马喽打金服
3 篇文章
×
发送私信
请先
登录
后发送私信
×
举报此文章
垃圾广告信息:
广告、推广、测试等内容
违规内容:
色情、暴力、血腥、敏感信息等内容
不友善内容:
人身攻击、挑衅辱骂、恶意行为
其他原因:
请补充说明
举报原因:
×
如果觉得我的文章对您有用,请随意打赏。你的支持将鼓励我继续创作!