奇安信攻防社区-CTF-RSA总结

CTF-RSA总结

RSA算法涉及三个参数,n,e,d，其中分为私钥和公钥，私钥是n,d，公钥是n,e。n是两个素数的乘积，一般这两个素数在RSA中用字母p,q表示。e是一个素数。d是e模 phi(n) 的逆元，d是由e,p,q可以求解出的。明文表示为m。然后通过RSA加密，得到密文C。

\[TOC\]

### RSA介绍

RSA算法涉及三个参数,n,e,d，其中分为私钥和公钥，私钥是n,d，公钥是n,e。n是两个素数的乘积，一般这两个素数在RSA中用字母p,q表示。e是一个素数。d是e模 phi(n) 的逆元，d是由e,p,q可以求解出的。明文表示为m。然后通过RSA加密，得到密文C。  
加密过程：  
c=m^e mod n

```php
c=pow(m,e,n)
```

解密过程：  
m=c^d mod n

```php
m=pow(c,d,n)
```

求解私钥d：

```php
d = gmpy2.invert(e, (p-1)*(q-1))
```

一般来说，n，e是公开的，但是由于n一般是两个大素数的乘积，所以我们很难求解出d，所以RSA加密就是利用现代无法快速实现大素数的分解，所存在的一种安全的非对称加密。

**应用流程**

1. 选取两个较大的互不相等的质数p和q，计算`n = p * q` 。
2. 计算`phi = (p-1) * (q-1)` 。
3. 选取任意e，使得e满足 `1<e<phi` 且 `gcd(e , phi) == 1` 。
4. 计算e关于 phi 的模逆元d， 即d满足`(e * d)% phi ==1` 。
5. 加解密：`c = (m ^ e) % n` ， `m = (c ^ d) % n` 。其中m为明文，c为密文，(n,e)为公钥对，d为私钥，要求 `0 <= m < n` 。

**理解模逆运算**

如果

```php
 (a*b)%c==1
```

那么a和b互为对方模c的模逆元/数论倒数

![mod_in v](https://shs3.b.qianxin.com/attack_forum/2021/12/attach-2c4ab8570b990e7e30110476d1eb89a113887835.png)

- 关于最大公约数有一个基本事实：`给予两整数a、c，必存在整数x、y使得ax + cy = gcd(a,c)` ，基于这个事实，当a,c互素即`gcd(a,c)==1` 时，有`ax+cy=1` ，那么就有`(a*x)%c==1` ，所以x就是a 对c的模逆元。因此，a对c存在模逆元b的充要条件是`gcd(a,c)==1` 。显然对于每一组`a,c` ，存在一种满足条件的x，在求模逆元时我们取得是最小正整数解`x mod n` 。
- 上述的基本事实很容易理解，因为a和c的最大公约数是gcd(a,b)，所以a和c都可表示为gcd(a,b)的整数倍，那么a和b的任意整系数的线性组合ax+by也必定能表示成gcd(a,c)的整数倍，他们当中最小的正整数就应该是gcd(a,c)。实际上最大公约数有一个定义就是：`a和b的最大公约数g是a和b的线性和中的最小正整数`。
- 求模逆元主要基于扩展欧几里得算法，贴一个Python实现：
    
    ```php
    def egcd ( a , b ):
       if (b == 0):
           return 1, 0, a
       else:
           x , y , q = egcd( b , a % b ) # q = GCD(a, b) = GCD(b, a%b)
           x , y = y, ( x - (a // b) * y )
           return x, y, q 
    def mod_inv(a,b):
      return egcd(a,b)[0]%b #求a模b得逆元
    ```
- 求模逆也可直接利用gmpy2库。如
    
    ```php
    import gmpy2;print gmpy2.invert(47,30)
    ```
    
    可求得47模30的逆为23。
    
    模意义下的运算法则

```php
(a + b) % n ≡ (a % n + b % n) % n
(a - b) % n ≡ (a % n - b % n) % n
(a * b) % n ≡ (a % n * b % n) % n
(a ^ b) % n ≡ ((a % n) ^ b) % n //幂运算

若 a ≡ b(mod n) ,则
1.对于任意正整数c,有a^c ≡ b^c(mod n)
2.对于任意整数c,有ac ≡ bc(mod n),a+c ≡ b+c(mod n),
3.若 c ≡ d(mod n),则a-c ≡ b-d(mod n),a+c ≡ b+d(mod n),ac ≡ bd(mod n)

如果ac≡bc (mod m)，且c和m互质，则a≡b (mod m）。
[理解：当且仅当c和m互质,c^-1存在,等式左右可同乘模逆。]

除法规则：
在模n意义下，a/b不再仅仅代表这两个数相除，而是指 a+k1*n 和 b+k2*n这两个组数中任意两个相除，使商为整数
因此也就可以理解，除以一个数等价于乘以它的逆
a/b ≡ c(mod n) <=> a ≡ c*(b^-1) (mod n)，其中b模n的逆记作b的负一次方。

费马小定理:
a是整数,p是质数,则a^p==a(mod p),如果a不是p的倍数,还有a^(p-1) ≡ 1(mod p) 
```

推荐文章 [模运算总结](https://blog.sengxian.com/algorithms/mod-world) 和 [取模运算涉及的算法](https://github.com/wujr5/algorithm-analysis-and-design/blob/master/relative-algorithm-learning/6-algorithm-about-modulo-operation.md) 。

**欧几里得算法**

欧几里得算法是求最大公约数的算法, 也就是中学学的 [辗转相除法](https://zh.wikipedia.org/wiki/%E8%BC%BE%E8%BD%89%E7%9B%B8%E9%99%A4%E6%B3%95) 。记 `gcd(a,b)` 为a和b的最大公约数，欧几里得算法的基本原理是`gcd(a,b)==gcd(b,a%b),(b!=0)` 和 `gcd(a,0)==a` 。

Python实现如下：

```php
# 递归版
def gcd(a, b):
    return a if not b else gcd(b, a % b)

# 迭代版
def gcd2(a, b):
    while b:
        a, b = b, a % b
    return a
```

**扩展欧几里得算法**

扩展欧几里得算法基于欧几里得算法，能够求出使得 `ax+by=gcd(a,b)` 的一组x,y。

[这篇文章](http://blog.miskcoo.com/2014/09/chinese-remainder-theorem#i-3) 解释得很到位，对照下图和以下递归版实现容易理解。

![ext_euclid](https://shs3.b.qianxin.com/attack_forum/2021/12/attach-f5c8d9577d5011acef615e3db1c60b2bf47c6ce3.png)

Python实现如下：

```php
# 递归版
def ext_euclid ( a , b ):
    # ref:https://zh.wikipedia.org/wiki/扩展欧几里得算法
    if (b == 0):
        return 1, 0, a
    else:
        x1 , y1 , q = ext_euclid( b , a % b ) # q = GCD(a, b) = GCD(b, a%b)
        x , y = y1, ( x1 - (a // b) * y1 )
        return x, y, q
# 迭代版
def egcd(a, b):
    # ref:https://blog.csdn.net/wyf12138/article/details/60476773
    if b == 0:
        return (1, 0, a)
    x, y = 0, 1
    s1, s2 = 1, 0
    r, q = a % b, a / b
    while r:
        m, n = x, y
        x = s1 - x * q
        y = s2 - y * q
        s1, s2 = m, n
        a, b = b, r
        r, q = a % b, a / b
    return (x, y, b)
```

**中国剩余定理**

[维基百科](https://zh.wikipedia.org/wiki/%E4%B8%AD%E5%9B%BD%E5%89%A9%E4%BD%99%E5%AE%9A%E7%90%86) 给出了简洁生动的说明:

![CRT](https://shs3.b.qianxin.com/attack_forum/2021/12/attach-3dc3dcc3389b205be105face5f7ebfde830eb8c5.png)

参考以上说明进行的Python实现:

```php
def CRT(mi, ai):
    # mi,ai分别表示模数和取模后的值,都为列表结构
    # Chinese Remainder Theorem
    # lcm=lambda x , y:x*y/gcd(x,y)
    # mul=lambda x , y:x*y
    # assert(reduce(mul,mi)==reduce(lcm,mi))
    # 以上可用于保证mi两两互质
    assert (isinstance(mi, list) and isinstance(ai, list))
    M = reduce(lambda x, y: x * y, mi)
    ai_ti_Mi = [a * (M / m) * gmpy2.invert(M / m, m) for (m, a) in zip(mi, ai)]
    return reduce(lambda x, y: x + y, ai_ti_Mi) % M
```

以上程序将mi当作两两互质处理,实际上有时会遇到其他情况，这时就需要逐一两两合并方程组。我参照下图实现了一个互质与不互质两种情况下都能工作良好的中国剩余定理（解同余方程组）的Python程序。

```php
def GCRT(mi, ai):
    # mi,ai分别表示模数和取模后的值,都为列表结构
    assert (isinstance(mi, list) and isinstance(ai, list))
    curm, cura = mi[0], ai[0]
    for (m, a) in zip(mi[1:], ai[1:]):
        d = gmpy2.gcd(curm, m)
        c = a - cura
        assert (c % d == 0) #不成立则不存在解
        K = c / d * gmpy2.invert(curm / d, m / d)
        cura += curm * K
        curm = curm * m / d
        cura %= curm
    return (cura % curm, curm) #(解,最小公倍数)
```

图片截自 [中国剩余定理（互质与不互质的情况）](https://blog.csdn.net/qq_29980371/article/details/71053219) 。

![CRT2](https://shs3.b.qianxin.com/attack_forum/2021/12/attach-4ff26e7198498c46a9133bffe197c30e05a636e8.png)

[CRT2](https://findneo.github.io/180727rsa-attack/1531591884497.png)

准备工具
----

- python 
    - gmpy2库
    - Windows：可从https://pypi.org/project/gmpy2/#files 直接下载已编译的安装包。
    - Linux： `sudo apt install python-gmpy2`
    - libnum库：
    - `git clone https://github.com/hellman/libnum.git &amp;&amp; cd libnum &amp;&amp; python setup.py install`
- yafu 
    - <https://sourceforge.net/projects/yafu/>
- RSATool2v17.exe

### 基础RSA加密脚本

```php
from Crypto.Util.number import *
import gmpy2

msg = 'flag is :testflag'
hex_msg=int(msg.encode("hex"),16)
print(hex_msg)
p=getPrime(100)
q=getPrime(100)
n=p*q
e=0x10001
phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)
print("d=",hex(d))
c=pow(hex_msg,e,n)
print("e=",hex(e))
print("n=",hex(n))
print("c=",hex(c))
```

rsa原理部分：[https://xz.aliyun.com/t/2446?utm\_source=tuicool&amp;amp;utm\_medium=referral](https://xz.aliyun.com/t/2446?utm_source=tuicool&amp;utm_medium=referral)

1.基础RSA解密脚本
-----------

```python
#!/usr/bin/env python
# -*- coding:utf-8 -*-
import binascii
import gmpy2
n=0x80b32f2ce68da974f25310a23144977d76732fa78fa29fdcbf
#这边我用yafu分解了n
p=780900790334269659443297956843
q=1034526559407993507734818408829
e=0x10001
c=0x534280240c65bb1104ce3000bc8181363806e7173418d15762

phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)
m=pow(c,d,n)
print(hex(m))
print(binascii.unhexlify(hex(m)[2:].strip("L")))
```

2.p和q相差过大或过小
------------

### 利用条件

因为n=p\*q  
其中若p和q的值相差较小，或者较大，都会造成n更容易分解的结果  
例如出题如下

```python
p=getPrime(512)
q=gmpy2.next_prime(p)
n=p*q
```

因为p和q十分接近，所以可以使用yafu直接分解

### yafu分解使用方法

使用

```php
factor(*)
```

括号中为要分解的数

```php
+ yafu-x64 "factor(@)" -batchfile pcat.txt

+ ~~~~~~~~
  + CategoryInfo          : ObjectNotFound: (yafu-x64:String) [], CommandNotFoundException
  + FullyQualifiedErrorId : CommandNotFoundException
  ~~~~~~~~

Suggestion [3,General]: 找不到命令 yafu-x64，但它确实存在于当前位置。默认情况下，Windows PowerShell 不会从当前位置加载命令。如果信任此命令，请改为键入“.\yafu-x64”。有关详细信息，请参阅 "get-help about_Command_Precedence"。
PS F:\mon0dy的工具包\编码与密码\密码\yafu-1.34> .\yafu-x64 "factor(@)" -batchfile pcat.txt

=== Starting work on batchfile expression ===

factor(636585149594574746909030160182690866222909256464847291783000651837227921337237899651287943597773270944384034858925295744880727101606841413640006527614873110651410155893776548737823152943797884729130149758279127430044739254000426610922834573094957082589539445610828279428814524313491262061930512829074466232633130599104490893572093943832740301809630847541592548921200288222432789208650949937638303429456468889100192613859073752923812454212239908948930178355331390933536771065791817643978763045030833712326162883810638120029378337092938662174119747687899484603628344079493556601422498405360731958162719296160584042671057160241284852522913676264596201906163)
=============================================

fac: factoring 636585149594574746909030160182690866222909256464847291783000651837227921337237899651287943597773270944384034858925295744880727101606841413640006527614873110651410155893776548737823152943797884729130149758279127430044739254000426610922834573094957082589539445610828279428814524313491262061930512829074466232633130599104490893572093943832740301809630847541592548921200288222432789208650949937638303429456468889100192613859073752923812454212239908948930178355331390933536771065791817643978763045030833712326162883810638120029378337092938662174119747687899484603628344079493556601422498405360731958162719296160584042671057160241284852522913676264596201906163
fac: using pretesting plan: normal
fac: no tune info: using qs/gnfs crossover of 95 digits
div: primes less than 10000
fmt: 1000000 iterations
Total factoring time = 11.8783 seconds

***factors found***

P327 = 797862863902421984951231350430312260517773269684958456342860983236184129602390919026048496119757187702076499551310794177917920137646835888862706126924088411570997141257159563952725882214181185531209186972351469946269508511312863779123205322378452194261217016552527754513215520329499967108196968833163329724620251096080377748737
P327 = 797862863902421984951231350430312260517773269684958456342860983236184129602390919026048496119757187702076499551310794177917920137646835888862706126924088411570997141257159563952725882214181185531209186972351469946269508511312863779123205322378452194261217016552527754513215520329499967108196968833163329724620251096080377747699

ans = 1

eof; done processing batchfile
PS F:\mon0dy的工具包\编码与密码\密码\yafu-1.34>
```

### 在线网站分解

<http://factordb.com/>  
通过在此类网站上查询n，如果可以分解或者之前分解成功过，那么可以直接得到p和q

![img](https://shs3.b.qianxin.com/attack_forum/2021/12/attach-d093a18797c1e80eb560d9da3bad8666e63b7f2b.png)

3.公约数分解n
--------

### 利用条件

当题目给的多对公钥n是公用了一个素数因子的时候，可以尝试公约数分解  
出题一般如下

```php
p1=getPrime(512)
p2=getPrime(512)
q=getPrime(512)
n1=p1*q
n2=p2*q
```

所以当题目给了多个n，并且发现n无法分解，可以尝试是否有公约数。

### 欧几里得辗转相除法

求公约数可以使用欧几里得辗转相除法，实现python脚本如下

```python
def gcd(a, b):   #求最大公约数
    if a < b:
        a, b = b, a
    while b != 0:
        temp = a % b
        a = b
        b = temp
    return a
```

### 用例

```python
def gcd(a, b):   #求最大公约数
    if a < b:
        a, b = b, a
    while b != 0:
        temp = a % b
        a = b
        b = temp
    return a

n1=0x6c9fb4bf11344e4c818be178e3d3db352797099f929e4ba8fa86d9c4ce3d8f71e3daa8c795b67dc2dabe1e1608836904386c364ecec759c27eaa83eb93710003d4cc848e558f7b11372405c5787b60eca627372767455a5fcf30cb6c157ca5a6267d63ffa16fe49e7433136a47945de2219f46a35f2b6a58196057c602e72a0b
n2=0x46733cc071bdee0d178fb32836a6b0a2f145a681df47d31ea9d9fc5b5fa0cc7ddbcd34531aefeace9840fc890f7a111f73593c9a41886b9a6f91cde3e6f9c71821a8ad877de51f78094599209746e80635c5625459ad7ba14f926b74875c8980a9436d6bbd54e1d9da72ae200383516098c04e24f58b23b4a8142cef0c931a55
print(gcd(n1,n2))
```

使用欧几里得辗转相除得到共有的因子，然后n1和n2除以这个因子，即可得到另一个素数因子。

4.模数分解(已知e,d,n求p,q)
-------------------

### 场景

已知e,d,n求p,q  
例如

```python
('d=', '0x455e1c421b78f536ec24e4a797b5be78df09d8d9e3b7f4e2244138a7583e810adf6ad056bb59a91300c9ead5ed77ea6bafdebf7ab2d9ec200127901083c7ffca45e83f2c934358366a2b6207b96a0eae6df0476060c063c281512834a42350a3b56bc09f5cec1a6975257d7f12a58f6389060e49b41f05e88ea2b30b395f6391')
('e=', '0x10001')
('n=', '0x71ee0f4883690893ab503e97e25e6308d4c1e0a050cbea7b9c040f7a5b5b484afcecc8a9b3cc6bf089a1e83281562df217caab7220e3dfc14399139ce437af2f131f9345675e4d848cfab5827818eeab7834374be4a0513f81f3df125a932c2bb4c24c834d798bcc80f9c4a8770b01f8e54620b72a4f0491edd391e635d48e71L')
```

### 模数分解

私钥d的获取是通过

```php
d = gmpy2.invert(e, (p-1)*(q-1))
```

分解p,q python实现如下

```python
import random  
def gcd(a, b):  
   if a < b:  
     a, b = b, a  
   while b != 0:  
     temp = a % b  
     a = b  
     b = temp  
   return a  
def getpq(n,e,d):  
    p = 1  
    q = 1  
    while p==1 and q==1:  
        k = d * e - 1  
        g = random.randint ( 0 , n )  
        while p==1 and q==1 and k % 2 == 0:  
            k /= 2  
            y = pow(g,k,n)  
            if y!=1 and gcd(y-1,n)>1:  
                p = gcd(y-1,n)  
                q = n/p  
    return p,q
```

### 完整用例

```python
import random  
def gcd(a, b):  
   if a < b:  
     a, b = b, a  
   while b != 0:  
     temp = a % b  
     a = b  
     b = temp  
   return a  
def getpq(n,e,d):
    p = 1  
    q = 1  
    while p==1 and q==1:  
        k = d * e - 1  
        g = random.randint ( 0 , n )  
        while p==1 and q==1 and k % 2 == 0:  
            k /= 2  
            y = pow(g,k,n)  
            if y!=1 and gcd(y-1,n)>1:  
                p = gcd(y-1,n)  
                q = n/p  
    return p,q

n=0x71ee0f4883690893ab503e97e25e6308d4c1e0a050cbea7b9c040f7a5b5b484afcecc8a9b3cc6bf089a1e83281562df217caab7220e3dfc14399139ce437af2f131f9345675e4d848cfab5827818eeab7834374be4a0513f81f3df125a932c2bb4c24c834d798bcc80f9c4a8770b01f8e54620b72a4f0491edd391e635d48e71
e=0x10001
d=0x455e1c421b78f536ec24e4a797b5be78df09d8d9e3b7f4e2244138a7583e810adf6ad056bb59a91300c9ead5ed77ea6bafdebf7ab2d9ec200127901083c7ffca45e83f2c934358366a2b6207b96a0eae6df0476060c063c281512834a42350a3b56bc09f5cec1a6975257d7f12a58f6389060e49b41f05e88ea2b30b395f6391
p,q=getpq(n,e,d)
print("p=",p)
print("q=",q)
print(p*q==n)
```

5.dp&amp;dq泄露
-------------

首先了解一下什么是dp、dq

```php
dp=d%(p-1)
dq=d%(q-1)
```

这种参数是为了让解密的时候更快速产生的

### 场景

假设题目仅给出p，q，dp，dq，c，即不给公钥e

```python
('p=', '0xf85d730bbf09033a75379e58a8465f8048b8516f8105ce2879ce774241305b6eb4ea506b61eb7e376d4fcd425c76e80cb748ebfaf3a852b5cf3119f028cc5971L')
('q=', '0xc1f34b4f826f91c5d68c5751c9af830bc770467a68699991be6e847c29c13170110ccd5e855710950abab2694b6ac730141152758acbeca0c5a51889cbe84d57L')
('dp=', '0xf7b885a246a59fa1b3fe88a2971cb1ee8b19c4a7f9c1a791b9845471320220803854a967a1a03820e297c0fc1aabc2e1c40228d50228766ebebc93c97577f511')
('dq=', '0x865fe807b8595067ff93d053cc269be6a75134a34e800b741cba39744501a31cffd31cdea6078267a0bd652aeaa39a49c73d9121fafdfa7e1131a764a12fdb95')
('c=', '0xae05e0c34e2ba4ca3536987cc2cfc3f1f7f53190164d0ac50b44832f0e7224c6fdeebd2c91e3991e7d179c26b1b997295dc9724925ba431f527fba212703a0d14a34ce133661ae0b6001ee326303d6ccdc27dbd94e0987fae25a84f197c1535bdac9094bfb3846b7ca696b2e5082bea7bff804da275772ca05dd51b185a4fc30L')
```

解密代码如下

```php
InvQ=gmpy2.invert(q,p)
mp=pow(c,dp,p)
mq=pow(c,dq,q)
m=(((mp-mq)*InvQ)%p)*q+mq
print '{:x}'.format(m).decode('hex')
```

### 解题完整脚本

```python
import gmpy2
import binascii
def decrypt(dp,dq,p,q,c):
    InvQ = gmpy2.invert(q,p)
    mp = pow(c,dp,p)
    mq = pow(c,dq,q)
    m=(((mp-mq)*InvQ)%p)*q+mq
    print (binascii.unhexlify(hex(m)[2:]))

p=0xf85d730bbf09033a75379e58a8465f8048b8516f8105ce2879ce774241305b6eb4ea506b61eb7e376d4fcd425c76e80cb748ebfaf3a852b5cf3119f028cc5971
q=0xc1f34b4f826f91c5d68c5751c9af830bc770467a68699991be6e847c29c13170110ccd5e855710950abab2694b6ac730141152758acbeca0c5a51889cbe84d57
dp=0xf7b885a246a59fa1b3fe88a2971cb1ee8b19c4a7f9c1a791b9845471320220803854a967a1a03820e297c0fc1aabc2e1c40228d50228766ebebc93c97577f511
dq=0x865fe807b8595067ff93d053cc269be6a75134a34e800b741cba39744501a31cffd31cdea6078267a0bd652aeaa39a49c73d9121fafdfa7e1131a764a12fdb95
c=0xae05e0c34e2ba4ca3536987cc2cfc3f1f7f53190164d0ac50b44832f0e7224c6fdeebd2c91e3991e7d179c26b1b997295dc9724925ba431f527fba212703a0d14a34ce133661ae0b6001ee326303d6ccdc27dbd94e0987fae25a84f197c1535bdac9094bfb3846b7ca696b2e5082bea7bff804da275772ca05dd51b185a4fc30
decrypt(dp,dq,p,q,c)
```

6.dp泄露
------

### 场景介绍

假设题目给出公钥n,e以及dp

```python
('dp=', '0x7f1344a0b8d2858492aaf88d692b32c23ef0d2745595bc5fe68de384b61c03e8fd054232f2986f8b279a0105b7bee85f74378c7f5f35c3fd505e214c0738e1d9')
('n=', '0x5eee1b4b4f17912274b7427d8dc0c274dc96baa72e43da36ff39d452ff6f2ef0dc6bf7eb9bdab899a6bb718c070687feff517fcf5377435c56c248ad88caddad6a9cefa0ca9182daffcc6e48451d481f37e6520be384bedb221465ec7c95e2434bf76568ef81e988039829a2db43572e2fe57e5be0dc5d94d45361e96e14bd65L')
('e=', '0x10001')
('c=', '0x510fd8c3f6e21dfc0764a352a2c7ff1e604e1681a3867480a070a480f722e2f4a63ca3d7a92b862955ab4be76cde43b51576a128fba49348af7a6e34b335cfdbda8e882925b20503762edf530d6cd765bfa951886e192b1e9aeed61c0ce50d55d11e343c78bb617d8a0adb7b4cf3b913ee85437191f1136e35b94078e68bee8dL')
```

给出密文要求解明文  
我们可以通过n，e，dp求解私钥d

### 求解公式推导

公式推导参考简书  
<https://www.jianshu.com/p/74270dc7a14b>  
首先dp是

```php
dp=d%(p-1)
```

以下推导过程如果有问题欢迎指正  
现在我们可以知道的是

```php
c≡m^e mod n
m≡c^d mod n
ϕ(n)=(p−1)∗(q−1)
d∗e≡1 mod ϕ(n)
dp≡d mod (p−1)
```

由上式可以得到

```php
dp∗e≡d∗e mod (p−1)
```

因此可以得到

```php
d∗e=k∗(p−1)+dp∗ed∗e≡1 mod ϕ(n)
```

我们将式1带入式2可以得到

```php
k∗(p−1)+dp∗e≡1 mod (p−1)∗(q−1)
```

故此可以得到

```php
k2∗(p−1)∗(q−1)+1=k1∗(p−1)+dp∗e
```

变换一下

```php
(p−1)∗[k2∗(q−1)−k1]+1=dp∗e
```

因为

```php
dp<p−1
```

可以得到

```php
e>k2∗(q−1)−k1
```

我们假设

```php
x=k2∗(q−1)−k1
```

可以得到x的范围为

```php
(0,e)
```

因此有

```php
x∗(p−1)+1=dp∗e
```

那么我们可以遍历

```php
x∈(0,e)
```

求出p-1，求的方法也很简单，遍历65537种可能，其中肯定有一个p可以被n整除那么求出p和q，即可利用

```php
ϕ(n)=(p−1)∗(q−1)d∗e≡1 mod ϕ(n)
```

推出

```php
d≡1∗e−1 mod ϕ(n)
```

注：这里的-1为逆元，不是倒数的那个-1

### 公式的python实现

求解私钥d脚本如下

```php
def getd(n,e,dp):
    for i in range(1,e):
        if (dp*e-1)%i == 0:
            if n%(((dp*e-1)/i)+1)==0:
                p=((dp*e-1)/i)+1
                q=n/(((dp*e-1)/i)+1)
                phi = (p-1)*(q-1)
                d = gmpy2.invert(e,phi)%phi
                return d
```

### 解题完整脚本

```php
import gmpy2
import binascii

def getd(n,e,dp):
    for i in range(1,e):
        if (dp*e-1)%i == 0:
            if n%(((dp*e-1)/i)+1)==0:
                p=((dp*e-1)/i)+1
                q=n/(((dp*e-1)/i)+1)
                phi = (p-1)*(q-1)
                d = gmpy2.invert(e,phi)%phi
                return d

dp=0x7f1344a0b8d2858492aaf88d692b32c23ef0d2745595bc5fe68de384b61c03e8fd054232f2986f8b279a0105b7bee85f74378c7f5f35c3fd505e214c0738e1d9
n=0x5eee1b4b4f17912274b7427d8dc0c274dc96baa72e43da36ff39d452ff6f2ef0dc6bf7eb9bdab899a6bb718c070687feff517fcf5377435c56c248ad88caddad6a9cefa0ca9182daffcc6e48451d481f37e6520be384bedb221465ec7c95e2434bf76568ef81e988039829a2db43572e2fe57e5be0dc5d94d45361e96e14bd65
e=0x10001
c=0x510fd8c3f6e21dfc0764a352a2c7ff1e604e1681a3867480a070a480f722e2f4a63ca3d7a92b862955ab4be76cde43b51576a128fba49348af7a6e34b335cfdbda8e882925b20503762edf530d6cd765bfa951886e192b1e9aeed61c0ce50d55d11e343c78bb617d8a0adb7b4cf3b913ee85437191f1136e35b94078e68bee8d

d=getd(n,e,dp)
m=pow(c,d,n)
print (binascii.unhexlify(hex(m)[2:]))
```

7.e与φ(n)不互素(n1n2e1e2c1c2)
-------------------------

### 场景介绍

假设题目给出两组公钥n,e以及第一组、第二组加密后的密文

```php
('n1=', '0xbf510b8e2b169fbce366eb15a4f6c71b370f02f2108c7feb482234a386185bce1a740fa6498e04edbdf2a639e320619d9f39d3e740ebaf578af0426bc3e851001a1d599108a08725347f6680a7f5581a32d91505023701872c3df723e8de9f201d3b17059bebff944b915045870d757eb6d6d009eb4561cc7e4b89968e4433a9L')
('e1=', '0x15d6439c6')
('c1=', '0x43e5cc4c99c3040aef2ccb0d4c45266f6b75cd7f9f1be105766689283f0886061c9cd52ac2b2b6c1b7d250c2079f354ca9b988db5556336201f3b5e489916b3b60b80c34bef8f608d7471fafaf14bee421b60630f42c5cc813356e786ff10e5efa334b8a73b7ea06afa6043f33be6a31010d306ba60516243add65c183da843aL')
('n2=', '0xba85d38d1bfc3fb281927c9246b5b771ac3344ca9fe1c2d9c793a886bffb5c84558f4a578cd5ba9e777a4e08f66d0cabe05b9aa2ae8d075778b5fbfff318a7f9b6f22e2eff6f79d8c1148941b3974f3e83a4a4f1520ad42336eddc572ec7ea04766eb798b2f1b1b52009b3eeea7741b2c55e3c7c11c5cf6a4e204c6b0d312f49L')
('e2=', '0x2c09848c6')
('c2=', '0x79ec6350649377f69b475eca83a7d9d5356a1d62e29933e9c8e2b19b4b23626a581037aba3be6d7f73d5bed049350e41c1ed4cdc3e10ee34ec576ef3449be2f7d930c759612e1c23c4db71d0e5185a80b548031e3857dd93eca4af017fcd25895fcc4e8a2b36c1dd36b8cd9cc9200e2879f025928fe346e2cfae5200e66de6ccL')
```

首先用公约数分解可以分解得到n1、n2的因子  
但是发现e和φ(n)是不互为素数的，所以我们无法求出私钥d。

### 解题公式推导

```php
gcd(e1,(p-1)*(q1-1))
gcd(e2,(p-1)*(q2-1))
```

得到结果为79858  
也就是说，e和φ(n)不互素且具有公约数79858

1、首先我们发现n1、n2可以用公约数分解出p、q  
但是由于e与φ(n)不互素，所以我们无法求解得到私钥d  
只有当他们互素时，才能保证e的逆元d唯一存在。  
公式推导过程参考博客  
<https://blog.csdn.net/chenzzhenguo/article/details/94339659>

2、下面进行等式运算，来找到解题思路  
还是要求逆元，则要找到与φ(n)互素的数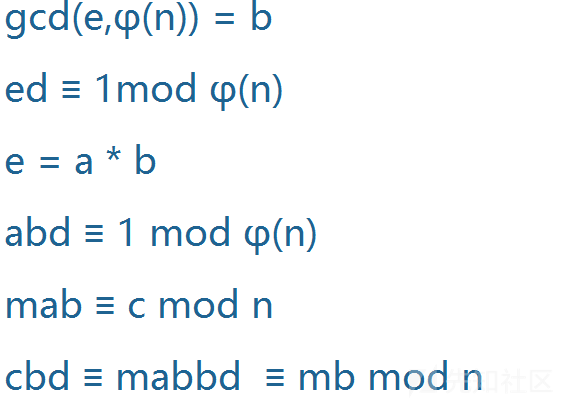

![img](https://shs3.b.qianxin.com/attack_forum/2021/12/attach-8f7a6a649d8dac59d493f4b198fd7f9ae042a1cb.png)

我们已知b=79858  
从上面的推算，可得a与φ(n)互素，于是可唯一确定bd  
于是求出bd  
gmpy2.invert(a,φ(n))  
然后想到bd/b，求出d，然后求明文。可是，经测试求出的是乱码，这个d不是我们想要的

3、想一下，给两组数据，应该有两组数据的作用，据上面的结论，我们可以得到一个同余式组

![img](https://shs3.b.qianxin.com/attack_forum/2021/12/attach-c12bb745dad56f8bdaf8a993b169cb68c8cb431d.png)

进一步推导

![img](https://shs3.b.qianxin.com/attack_forum/2021/12/attach-0043c9476b20cb7ba15a6dda1a4edd4f860c0671.png)

可以计算出特解m  
m=solve\_crt(\[m1,m2,m3\], \[q1,q2,p\])  
我们想到模n1,n2不行那模q1\*q2呢，  
这里res可取特值m

![img](https://shs3.b.qianxin.com/attack_forum/2021/12/attach-445e100bcb2fece6360e864c0b7db237551eab05.png)

那么问题就转化为求一个新的rsa题目  
e=79858，经计算发现此时e与φ(n)=(q1-1)(q2-1)，还是有公因数2。  
那么，我们参照上述思路，可得出m^2，此时直接对m开方即可。

![img](https://shs3.b.qianxin.com/attack_forum/2021/12/attach-84975a91472028d79431ba0c6a23867519ae76d4.png)

### 完整解题脚本

```php
#!/usr/bin/env python
# -*- coding:utf-8 -*-
import gmpy2
import binascii

def gcd(a, b):
    if a < b:
        a, b = b, a
    while b != 0:
        temp = a % b
        a = b
        b = temp
    return a

n1=0xbf510b8e2b169fbce366eb15a4f6c71b370f02f2108c7feb482234a386185bce1a740fa6498e04edbdf2a639e320619d9f39d3e740ebaf578af0426bc3e851001a1d599108a08725347f6680a7f5581a32d91505023701872c3df723e8de9f201d3b17059bebff944b915045870d757eb6d6d009eb4561cc7e4b89968e4433a9
n2=0xba85d38d1bfc3fb281927c9246b5b771ac3344ca9fe1c2d9c793a886bffb5c84558f4a578cd5ba9e777a4e08f66d0cabe05b9aa2ae8d075778b5fbfff318a7f9b6f22e2eff6f79d8c1148941b3974f3e83a4a4f1520ad42336eddc572ec7ea04766eb798b2f1b1b52009b3eeea7741b2c55e3c7c11c5cf6a4e204c6b0d312f49

p=gcd(n1,n2)
q1=n1//p
q2=n2//p

c1=0x43e5cc4c99c3040aef2ccb0d4c45266f6b75cd7f9f1be105766689283f0886061c9cd52ac2b2b6c1b7d250c2079f354ca9b988db5556336201f3b5e489916b3b60b80c34bef8f608d7471fafaf14bee421b60630f42c5cc813356e786ff10e5efa334b8a73b7ea06afa6043f33be6a31010d306ba60516243add65c183da843a
c2=0x79ec6350649377f69b475eca83a7d9d5356a1d62e29933e9c8e2b19b4b23626a581037aba3be6d7f73d5bed049350e41c1ed4cdc3e10ee34ec576ef3449be2f7d930c759612e1c23c4db71d0e5185a80b548031e3857dd93eca4af017fcd25895fcc4e8a2b36c1dd36b8cd9cc9200e2879f025928fe346e2cfae5200e66de6cc
e1 =0x15d6439c6
e2 =0x2c09848c6

#print(gcd(e1,(p-1)*(q1-1)))
#print(gcd(e2,(p-1)*(q2-1)))

e1=e1//gcd(e1,(p-1)*(q1-1))
e2=e2//gcd(e2,(p-1)*(q2-1))

phi1=(p-1)*(q1-1);phi2=(p-1)*(q2-1)
d1=gmpy2.invert(e1,phi1)
d2=gmpy2.invert(e2,phi2)
f1=pow(c1,d1,n1)
f2=pow(c2,d2,n2)

def GCRT(mi, ai):
    curm, cura = mi[0], ai[0]
    for (m, a) in zip(mi[1:], ai[1:]):
        d = gmpy2.gcd(curm, m)
        c = a - cura
        K = c // d * gmpy2.invert(curm // d, m // d)
        cura += curm * K
        curm = curm * m // d
        cura %= curm
    return (cura % curm, curm)

f3,lcm = GCRT([n1,n2],[f1,f2])
n3=q1*q2
c3=f3%n3
phi3=(q1-1)*(q2-1)

d3=gmpy2.invert(39929,phi3)#39929是79858//gcd((q1-1)*(q2-1),79858) 因为新的e和φ(n)还是有公因数2
m3=pow(c3,d3,n3)

if gmpy2.iroot(m3,2)[1] == 1:
    flag=gmpy2.iroot(m3,2)[0]
    print(binascii.unhexlify(hex(flag)[2:].strip("L")))
```

8.公钥n由多个素数因子组成
--------------

### 场景介绍

题目如下

```php
('n=', '0xf1b234e8a03408df4868015d654dcb931f038ef4fc0be8658c9b951ee6c60d23689a1bfb151e74df0910fa1cf8a542282a65')
('e=', '0x10001')
('c=', '0x22fda6137013bac19754f78e8d9658498017f05a4b0814f2af97dc2c60fdc433d2949ea27b13337961ef3c4cf27452ad3c95')
```

因为这题的公钥n是由四个素数相乘得来的，  
其中四个素数的值相差较小，或者较大，都会造成n更容易分解的结果  
例如出题如下

```php
p=getPrime(100)
q=gmpy2.next_prime(p)
r=gmpy2.next_prime(q)
s=gmpy2.next_prime(r)
n=p*q*r*s
```

因为p、q、r、s十分接近，所以可以使用yafu直接分解

### yafu分解

使用

```php
factor(*)
```

括号中为要分解的数

### 公钥n由多素数相乘解题脚本

```php
import binascii
import gmpy2
p=1249559655343546956371276497499
q=1249559655343546956371276497489
r=1249559655343546956371276497537
s=1249559655343546956371276497423
e=0x10001
c=0x22fda6137013bac19754f78e8d9658498017f05a4b0814f2af97dc2c60fdc433d2949ea27b13337961ef3c4cf27452ad3c95
n=p*q*r*s

phi=(p-1)*(q-1)*(r-1)*(s-1)
d=gmpy2.invert(e,phi)
m=pow(c,d,n)
print(binascii.unhexlify(hex(m)[2:].strip("L")))
```

```python
from random import randint
from gmpy2 import *
from Crypto.Util.number import *

def getprime(bits):
    while 1:
        n = 1
        while n.bit_length() < bits:
            n *= next_prime(randint(1,1000))
        if isPrime(n - 1):
            return n - 1

m = bytes_to_long(b'flag{************************************}')

p = getprime(505)
q = getPrime(512)
r = getPrime(512)
assert m < q

n = p * q * r
e = 0x10001
d = invert(q ** 2, p ** 2)
c = pow(m, 2, r)
cipher = pow(c, e, n)

print(n)
print(d)
print(cipher)

'''

7941371739956577280160664419383740967516918938781306610817149744988379280561359039016508679365806108722198157199058807892703837558280678711420411242914059658055366348123106473335186505617418956630780649894945233345985279471106888635177256011468979083320605103256178446993230320443790240285158260236926519042413378204298514714890725325831769281505530787739922007367026883959544239568886349070557272869042275528961483412544495589811933856131557221673534170105409
7515987842794170949444517202158067021118454558360145030399453487603693522695746732547224100845570119375977629070702308991221388721952258969752305904378724402002545947182529859604584400048983091861594720299791743887521228492714135449584003054386457751933095902983841246048952155097668245322664318518861440
1618155233923718966393124032999431934705026408748451436388483012584983753140040289666712916510617403356206112730613485227084128314043665913357106301736817062412927135716281544348612150328867226515184078966397180771624148797528036548243343316501503364783092550480439749404301122277056732857399413805293899249313045684662146333448668209567898831091274930053147799756622844119463942087160062353526056879436998061803187343431081504474584816590199768034450005448200

'''

```

```python
import gmpy2
import binascii
from sympy.ntheory.residue_ntheory import nthroot_mod
from Crypto.Util.number import *
p=102634610559478918970860957918259981057327949366949344137104804864768237961662136189827166317524151288799657758536256924609797810164397005081733039415393
q=7534810196420932552168708937019691994681052660068275906973480617604535381306041583841106383688654426129050931519275383386503174076258645141589911492908993
r=10269028767754306217563721664976261924407940883784193817786660413744866184645984238866463711873380072803747092361041245422348883639933712733051005791543841
e=0x10001
cipher=1618155233923718966393124032999431934705026408748451436388483012584983753140040289666712916510617403356206112730613485227084128314043665913357106301736817062412927135716281544348612150328867226515184078966397180771624148797528036548243343316501503364783092550480439749404301122277056732857399413805293899249313045684662146333448668209567898831091274930053147799756622844119463942087160062353526056879436998061803187343431081504474584816590199768034450005448200
n=p*q*r

phi=(p-1)*(q-1)*(r-1)
d=gmpy2.invert(e,phi)
c = gmpy2.powmod(cipher,d,n)#cipher = pow(c, e, n)
m = nthroot_mod(c,2,r)#c = pow(m, 2, r)
print(binascii.unhexlify(hex(m)[2:].strip("L")))
```

9.小明文攻击(e很小)
------------

小明文攻击是基于低加密指数的，主要分成两种情况。

### 明文过小，导致明文的e次方仍然小于n

```php
('n=', '0xad03794ef170d81aad370dccb7b92af7d174c10e0ae9ddc99b7dc5f93af6c65b51cc9c40941b002c7633caf8cd50e1b73aa942c8488d46c0032064306de388151814982b6d35b4e2a62dd647f527b31b4f826c36848dc52999574a8694460e1b59b4e96bda1341d3ba5f991f0000a56004d47681ecfd37a5e64bd198617f8dadL')
('e=', '0x3')
('c=', '0x10652cdf6f422470ea251f77L')
```

这种情况直接对密文e次开方，即可得到明文

解题脚本

```php
import binascii
import gmpy2
n=0xad03794ef170d81aad370dccb7b92af7d174c10e0ae9ddc99b7dc5f93af6c65b51cc9c40941b002c7633caf8cd50e1b73aa942c8488d46c0032064306de388151814982b6d35b4e2a62dd647f527b31b4f826c36848dc52999574a8694460e1b59b4e96bda1341d3ba5f991f0000a56004d47681ecfd37a5e64bd198617f8dad
e=0x3
c=0x10652cdf6f422470ea251f77

m=gmpy2.iroot(c, 3)[0]
print(binascii.unhexlify(hex(m)[2:].strip("L")))
```

### 明文的三次方虽然比n大，但是大不了多少

```php
('n=', '0x9683f5f8073b6cd9df96ee4dbe6629c7965e1edd2854afa113d80c44f5dfcf030a18c1b2ff40575fe8e222230d7bb5b6dd8c419c9d4bca1a7e84440a2a87f691e2c0c76caaab61492db143a61132f584ba874a98363c23e93218ac83d1dd715db6711009ceda2a31820bbacaf1b6171bbaa68d1be76fe986e4b4c1b66d10af25L')
('e=', '0x3')
('c=', '0x8541ee560f77d8fe536d48eab425b0505e86178e6ffefa1b0c37ccbfc6cb5f9a7727baeb3916356d6fce3205cd4e586a1cc407703b3f709e2011d7b66eaaeea9e381e595b4d515c433682eb3906d9870fadbffd0695c0168aa26447f7a049c260456f51e937ce75b74e5c3c2bd7709b981898016a3a18f15ae99763ff40805aaL')
```

爆破即可，每次加上一个n

```php
i = 0
while 1:
    res = iroot(c+i*n,3)
    if(res[1] == True):
        print res
        break
    print "i="+str(i)
    i = i+1
```

完整脚本

```python
import binascii
import gmpy2

n=0x9683f5f8073b6cd9df96ee4dbe6629c7965e1edd2854afa113d80c44f5dfcf030a18c1b2ff40575fe8e222230d7bb5b6dd8c419c9d4bca1a7e84440a2a87f691e2c0c76caaab61492db143a61132f584ba874a98363c23e93218ac83d1dd715db6711009ceda2a31820bbacaf1b6171bbaa68d1be76fe986e4b4c1b66d10af25
e=0x3
c=0x8541ee560f77d8fe536d48eab425b0505e86178e6ffefa1b0c37ccbfc6cb5f9a7727baeb3916356d6fce3205cd4e586a1cc407703b3f709e2011d7b66eaaeea9e381e595b4d515c433682eb3906d9870fadbffd0695c0168aa26447f7a049c260456f51e937ce75b74e5c3c2bd7709b981898016a3a18f15ae99763ff40805aa

i = 0
while 1:
    res = gmpy2.iroot(c+i*n,3)
    if(res[1] == True):
        m=res[0]
        print(binascii.unhexlify(hex(m)[2:].strip("L")))
        break
    print "i="+str(i)
    i = i+1
```

10.低加密指数广播攻击(明文一样，多组加密n1n2n3)
-----------------------------

### 场景介绍

如果选取的加密指数较低，并且使用了相同的加密指数给一个接受者的群发送相同的信息，那么可以进行广播攻击得到明文。  
这个识别起来比较简单，一般来说都是给了三组加密的参数和明密文，其中题目很明确地能告诉你这三组的明文都是一样的，并且e都取了一个较小的数字。

```php
('n=', '0x683fe30746a91545a45225e063e8dc64d26dbf98c75658a38a7c9dfd16dd38236c7aae7de5cbbf67056c9c57817fd3da79dc4955217f43caefde3b56a46acf5dL', 'e=', '0x7', 'c=', '0x673c72ace143441c07cba491074163c003f1a550eab56b1255e5ea9fa2bbd68fd6a9ccb48db9fd66d5dfc6a55c79cad3d9de53f700a1e3c2a29731dc56ba43cdL')
('n=', '0xa39292e6ad271bb6a2d1345940dfab8001a53d28bc7468f285d2873d784004c2653549c589dae91c6d8238977ff1c4bea4f17d424a0fc4d5587661cc7dde3a77L', 'e=', '0x7', 'c=', '0x6111357d180d966a495f38566ebe4ea51fa0d54159b22bbd443cde9387687d87c08638483b39221883453a5ad09f6a0e3726b214e8e333037d178a3d0f125343L')
('n=', '0x52c32366d84d34564a5fdc1650fc401c41ad2a63a2d6ef57c32c7887bb25da9d42c0acfb887c6334c938839c9a43aca93b2c7468915d1846576f92c342046d1fL', 'e=', '0x7', 'c=', '0x26cd2225c0229b6a3f1d1d685e53d114aa3d792737d040fbc14189336ac12fb780872792b0c0b259847badffd1427897ede0d60247aa5e79633f27ccb43e7cc2L')
```

### 解题脚本

```php
import binascii,gmpy2

n =  [
0x683fe30746a91545a45225e063e8dc64d26dbf98c75658a38a7c9dfd16dd38236c7aae7de5cbbf67056c9c57817fd3da79dc4955217f43caefde3b56a46acf5d,
0xa39292e6ad271bb6a2d1345940dfab8001a53d28bc7468f285d2873d784004c2653549c589dae91c6d8238977ff1c4bea4f17d424a0fc4d5587661cc7dde3a77,
0x52c32366d84d34564a5fdc1650fc401c41ad2a63a2d6ef57c32c7887bb25da9d42c0acfb887c6334c938839c9a43aca93b2c7468915d1846576f92c342046d1f
]
c =  [
0x673c72ace143441c07cba491074163c003f1a550eab56b1255e5ea9fa2bbd68fd6a9ccb48db9fd66d5dfc6a55c79cad3d9de53f700a1e3c2a29731dc56ba43cd,
0x6111357d180d966a495f38566ebe4ea51fa0d54159b22bbd443cde9387687d87c08638483b39221883453a5ad09f6a0e3726b214e8e333037d178a3d0f125343,
0x26cd2225c0229b6a3f1d1d685e53d114aa3d792737d040fbc14189336ac12fb780872792b0c0b259847badffd1427897ede0d60247aa5e79633f27ccb43e7cc2
]
def CRT(mi, ai):
    assert(reduce(gmpy2.gcd,mi)==1)
    assert (isinstance(mi, list) and isinstance(ai, list))
    M = reduce(lambda x, y: x * y, mi)
    ai_ti_Mi = [a * (M / m) * gmpy2.invert(M / m, m) for (m, a) in zip(mi, ai)]
    return reduce(lambda x, y: x + y, ai_ti_Mi) % M
e=0x7
m=gmpy2.iroot(CRT(n, c), e)[0]
print(binascii.unhexlify(hex(m)[2:].strip("L")))
```

11.低解密指数攻击(维纳攻击，e很大)
--------------------

### 场景介绍

主要利用的是私钥d很小，表现形式一般是e很大

```php
n = 9247606623523847772698953161616455664821867183571218056970099751301682205123115716089486799837447397925308887976775994817175994945760278197527909621793469
e = 27587468384672288862881213094354358587433516035212531881921186101712498639965289973292625430363076074737388345935775494312333025500409503290686394032069
```

### 攻击脚本

github上有开源的攻击代码https://github.com/pablocelayes/rsa-wiener-attack

求解得到私钥d，在用e,n,d正常求解

```python
def rational_to_contfrac (x, y):
    ''' 
    Converts a rational x/y fraction into
    a list of partial quotients [a0, ..., an] 
    '''
    a = x//y
    if a * y == x:
        return [a]
    else:
        pquotients = rational_to_contfrac(y, x - a * y)
        pquotients.insert(0, a)
        return pquotients
def convergents_from_contfrac(frac):    
    '''
    computes the list of convergents
    using the list of partial quotients 
    '''
    convs = [];
    for i in range(len(frac)):
        convs.append(contfrac_to_rational(frac[0:i]))
    return convs

def contfrac_to_rational (frac):
    '''Converts a finite continued fraction [a0, ..., an]
     to an x/y rational.
     '''
    if len(frac) == 0:
        return (0,1)
    elif len(frac) == 1:
        return (frac[0], 1)
    else:
        remainder = frac[1:len(frac)]
        (num, denom) = contfrac_to_rational(remainder)
        # fraction is now frac[0] + 1/(num/denom), which is 
        # frac[0] + denom/num.
        return (frac[0] * num + denom, num)

def egcd(a,b):
    '''
    Extended Euclidean Algorithm
    returns x, y, gcd(a,b) such that ax + by = gcd(a,b)
    '''
    u, u1 = 1, 0
    v, v1 = 0, 1
    while b:
        q = a // b
        u, u1 = u1, u - q * u1
        v, v1 = v1, v - q * v1
        a, b = b, a - q * b
    return u, v, a

def gcd(a,b):
    '''
    2.8 times faster than egcd(a,b)[2]
    '''
    a,b=(b,a) if a<b else (a,b)
    while b:
        a,b=b,a%b
    return a

def modInverse(e,n):
    '''
    d such that de = 1 (mod n)
    e must be coprime to n
    this is assumed to be true
    '''
    return egcd(e,n)[0]%n

def totient(p,q):
    '''
    Calculates the totient of pq
    '''
    return (p-1)*(q-1)

def bitlength(x):
    '''
    Calculates the bitlength of x
    '''
    assert x >= 0
    n = 0
    while x > 0:
        n = n+1
        x = x>>1
    return n

def isqrt(n):
    '''
    Calculates the integer square root
    for arbitrary large nonnegative integers
    '''
    if n < 0:
        raise ValueError('square root not defined for negative numbers')

if n == 0:
        return 0
    a, b = divmod(bitlength(n), 2)
    x = 2**(a+b)
    while True:
        y = (x + n//x)//2
        if y >= x:
            return x
        x = y

def is_perfect_square(n):
    '''
    If n is a perfect square it returns sqrt(n),

otherwise returns -1
    '''
    h = n &amp; 0xF; #last hexadecimal "digit"

if h > 9:
        return -1 # return immediately in 6 cases out of 16.

# Take advantage of Boolean short-circuit evaluation
    if ( h != 2 and h != 3 and h != 5 and h != 6 and h != 7 and h != 8 ):
        # take square root if you must
        t = isqrt(n)
        if t*t == n:
            return t
        else:
            return -1

return -1

def hack_RSA(e,n):
    frac = rational_to_contfrac(e, n)
    convergents = convergents_from_contfrac(frac)

for (k,d) in convergents:
        #check if d is actually the key
        if k!=0 and (e*d-1)%k == 0:
            phi = (e*d-1)//k
            s = n - phi + 1
            # check if the equation x^2 - s*x + n = 0
            # has integer roots
            discr = s*s - 4*n
            if(discr>=0):
                t = is_perfect_square(discr)
                if t!=-1 and (s+t)%2==0:
                    print("\nHacked!")
                    return d

def main():
    n = 9247606623523847772698953161616455664821867183571218056970099751301682205123115716089486799837447397925308887976775994817175994945760278197527909621793469
    e = 27587468384672288862881213094354358587433516035212531881921186101712498639965289973292625430363076074737388345935775494312333025500409503290686394032069
    d=hack_RSA(e,n)
    print ("d=")
    print (d)

if __name__ == '__main__':
    main()
```

脚本二：

```python
import ContinuedFractions, Arithmetic, RSAvulnerableKeyGenerator

def hack_RSA(e,n):
    '''
    Finds d knowing (e,n)
    applying the Wiener continued fraction attack
    '''
    frac = ContinuedFractions.rational_to_contfrac(e, n)
    convergents = ContinuedFractions.convergents_from_contfrac(frac)

for (k,d) in convergents:

#check if d is actually the key
        if k!=0 and (e*d-1)%k == 0:
            phi = (e*d-1)//k
            s = n - phi + 1
            # check if the equation x^2 - s*x + n = 0
            # has integer roots
            discr = s*s - 4*n
            if(discr>=0):
                t = Arithmetic.is_perfect_square(discr)
                if t!=-1 and (s+t)%2==0:
                    print("Hacked!")
                    return d

def main():
    n = 18462906143035540993814517057095163128283817787230664517838986634801013392767711846485937113330072380038567780269061919808605648774959966319179757205173372523095161810322702620470126948608656351385935375720727519176775110406692586449768317335765421930399299578230419560189633716571287406027463911286833332787737419540756653612611709926058384814812935770145166745335145087323852211057246522872067333040272572190577262813212787729743380140592301701193918348912668992966189995193003441075512789075254845693251194059243188025613215624222354768281910170062917473229700929505219308776883069798326608764552258161920559190481
    e = 14065324093316017945695720258347429532521523200228598193322667338820770590989154977786981894794588594064536009186732255775035804405327706425255296803855527639374329558376563095664859692148197185703687276097309462020144376262777557533944519562049109221719648126706993033163993490190085491702629251352329396471456129542825658446009162968346786594848548139595669836329358788165100849817671092568134531593182392252696719165573226130084180843486935720502707239300540428534291779101061922644007823991998086019198292035392258539304441052201138357754863223836486846439513422901513872417295274198920142360883876210212927825007
    d=hack_RSA(e,n)
    print ("d=")
    print (d)
```

12.共模攻击(e不同n相同m相同)
------------------

### 场景介绍

识别：若干次加密，e不同，n相同，m相同。就可以在不分解n和求d的前提下，解出明文m。

```python
('n=', '0xc42b9d872f8ecf90b4832199771bbd8d9bafb213747d905a644baa42144f316dc224e7914f8a5d361eeab930adf5ea7fbe1416e58b3fae34ca7e6d2a3145e04af02cf5a4f14539fff032bccd7bb9cf85b12d7d36dbc870b57e11aa5704304d08eff685fe4ccd707e308dfac6a1167d79199ffa9396c4f2efb4770256253d1407L')
('e1=', '0xc21000af014a98b2455dec479L')
('e2=', '0x9935842d63b75899ddd81b467L')
('c1=', '0xc0204d515a275954bbc8390d80efa1cca3bb29724ed7ba18f861913e28b6400298603b920d484284ad9c1c175587496300355395cb06b32603e779ec9b97f7eea6bb0de42c54f7f60e6e1171496efef0de8048e6074658084d080bd346db426888084e6dd45cb89b283247443de75328d47f9bd64adbd9be86043c6d13c7ed41L')
('c2=', '0xc4053ed3455c15174e5699ab6eb09b830a98b79e92e7518b713e828faca4d6d02306a65a8ec70893ca8a56943a7074e6de8649f099164cad33b8ca93fce1656f0712b990cce06642250c52a80d19c2afa94a4e158139028ac89c811e6be8d7b6984b6c1edcdd752e4955e3a6f1ab38cf2edb4474a80e03d6c313eb8ebf4e98ccL')
```

### 推导过程

```python
首先，两个加密指数互质：
gcd(e1,e2)=1

即存在s1、s2使得：
s1+*e1+s2*e2=1

又因为：
c1≡m^e1 mod n
c2≡m mod n

代入化简可得：
c1^s1 * c2^s2 ≡ m mod n

即可求出明文
```

公式的python实现如下

```python
def egcd(a, b):
    if a == 0:
      return (b, 0, 1)
    else:
      g, y, x = egcd(b % a, a)
      return (g, x - (b // a) * y, y)
def modinv(a, m):
    g, x, y = egcd(a, m)
    if g != 1:
      raise Exception('modular inverse does not exist')
    else:
      return x % m
s = egcd(e1, e2)
s1 = s[1]
s2 = s[2]
if s1<0:
   s1 = - s1
   c1 = modinv(c1, n)
elif s2<0:
   s2 = - s2
   c2 = modinv(c2, n)
m=(pow(c1,s1,n)*pow(c2,s2,n)) % n
```

### 完整解题脚本

```python
import sys
import binascii
sys.setrecursionlimit(1000000)
def egcd(a, b):
    if a == 0:
      return (b, 0, 1)
    else:
      g, y, x = egcd(b % a, a)
      return (g, x - (b // a) * y, y)
def modinv(a, m):
    g, x, y = egcd(a, m)
    if g != 1:
      raise Exception('modular inverse does not exist')
    else:
      return x % m

c1=0xc0204d515a275954bbc8390d80efa1cca3bb29724ed7ba18f861913e28b6400298603b920d484284ad9c1c175587496300355395cb06b32603e779ec9b97f7eea6bb0de42c54f7f60e6e1171496efef0de8048e6074658084d080bd346db426888084e6dd45cb89b283247443de75328d47f9bd64adbd9be86043c6d13c7ed41
n=0xc42b9d872f8ecf90b4832199771bbd8d9bafb213747d905a644baa42144f316dc224e7914f8a5d361eeab930adf5ea7fbe1416e58b3fae34ca7e6d2a3145e04af02cf5a4f14539fff032bccd7bb9cf85b12d7d36dbc870b57e11aa5704304d08eff685fe4ccd707e308dfac6a1167d79199ffa9396c4f2efb4770256253d1407
e1=0xc21000af014a98b2455dec479
c2=0xc4053ed3455c15174e5699ab6eb09b830a98b79e92e7518b713e828faca4d6d02306a65a8ec70893ca8a56943a7074e6de8649f099164cad33b8ca93fce1656f0712b990cce06642250c52a80d19c2afa94a4e158139028ac89c811e6be8d7b6984b6c1edcdd752e4955e3a6f1ab38cf2edb4474a80e03d6c313eb8ebf4e98cc
e2=0x9935842d63b75899ddd81b467

s = egcd(e1, e2)
s1 = s[1]
s2 = s[2]

if s1<0:
   s1 = - s1
   c1 = modinv(c1, n)
elif s2<0:
   s2 = - s2
   c2 = modinv(c2, n)
m=(pow(c1,s1,n)*pow(c2,s2,n)) % n
print(m)
print (binascii.unhexlify(hex(m)[2:].strip("L")))
```

```python
#python2
from gmpy2 import invert
def gongmogongji(n, c1, c2, e1, e2):
    def egcd(a, b):
        if b == 0:
            return a, 0
        else:
            x, y = egcd(b, a % b)
            return y, x - (a // b) * y
    s = egcd(e1, e2)
    s1 = s[0]
    s2 = s[1]
    if s1 < 0:
        s1 = - s1
        c1 = invert(c1, n)
    elif s2 < 0:
        s2 = - s2
        c2 = invert(c2, n)
    m = pow(c1, s1, n) * pow(c2, s2, n) % n
    return m

n= 6266565720726907265997241358331585417095726146341989755538017122981360742813498401533594757088796536341941659691259323065631249
e1= 773
e2= 839
c1= 3453520592723443935451151545245025864232388871721682326408915024349804062041976702364728660682912396903968193981131553111537349
c2= 5672818026816293344070119332536629619457163570036305296869053532293105379690793386019065754465292867769521736414170803238309535

result = gongmogongji(n, c1, c2, e1, e2)
print(result)
#1021089710312311910410111011910111610410511010710511610511511211111511510598108101125
#flag=hex(result)[2:].decode('hex')
result=str(result)
flag=""
i=0
while i < len(result):
    if result[i]=='1':
        c=chr(int(result[i:i+3]))
        i+=3
    else:
        c=chr(int(result[i:i+2]))
        i+=2
    flag+=c
print(flag)
```

13.Stereotyped messages攻击(给了m的高位)
---------------------------------

### 场景介绍

```php
('n=', '0xf85539597ee444f3fcad07142ecf6eaae5320301244a7cedc50b2beed7e60ffa11ccf28c1a590fb81346fb16b0cecd046a1f63f0bf93185c109b8c93068ec02fL')
('e=', '0x3')
('c=', '0xa75c3c8a19ed9c911d851917e442a8e7b425e4b7f92205ca532a2ab0f5abe6cb86d164cc61374877f9e88e7bca606b43c79f1d59deadfcc68c3db52e5fc42f0L')
('m=', '0x666c6167206973203a746573743132313131313131313131313133343536000000000000000000')
```

给了明文的高位，可以尝试使用Stereotyped messages攻击  
我们需要使用sage实现该算法  
可以安装SageMath  
或者在线网站https://sagecell.sagemath.org/

### 攻击脚本

```python
e = 0x3
b=0x666c6167206973203a746573743132313131313131313131313133343536000000000000000000
n = 0xf85539597ee444f3fcad07142ecf6eaae5320301244a7cedc50b2beed7e60ffa11ccf28c1a590fb81346fb16b0cecd046a1f63f0bf93185c109b8c93068ec02f
c=0xa75c3c8a19ed9c911d851917e442a8e7b425e4b7f92205ca532a2ab0f5abe6cb86d164cc61374877f9e88e7bca606b43c79f1d59deadfcc68c3db52e5fc42f0
kbits=72
PR.<x> = PolynomialRing(Zmod(n))
f = (x + b)^e-c
x0 = f.small_roots(X=2^kbits, beta=1)[0]
print "x: %s" %hex(int(x0))
```

可以求解出m的低位

14.Factoring with high bits known攻击(给出p的高位)
-------------------------------------------

### 场景介绍

```python
('n=', '0xb50193dc86a450971312d72cc8794a1d3f4977bcd1584a20c31350ac70365644074c0fb50b090f38d39beb366babd784d6555d6de3be54dad3e87a93a703abddL')
('p=', '0xd7e990dec6585656512c841ac932edaf048184bac5ebf9967000000000000000L')
('e=', '0x3')
('c=', '0x428a95e5712e8aa22f6d4c39ee5ec85f422608c2f141abf22799c1860a5e343068ab55dfb5c99a7085714f4ce8950e85d8ed0a11fce3516cf66a641dca8321eeL')
```

题目给出p的高位

### 攻击脚本

该后门算法依赖于Coppersmith partial information attack算法, sage实现该算法

```python
p = 0xd7e990dec6585656512c841ac932edaf048184bac5ebf9967000000000000000
n = 0xb50193dc86a450971312d72cc8794a1d3f4977bcd1584a20c31350ac70365644074c0fb50b090f38d39beb366babd784d6555d6de3be54dad3e87a93a703abdd

kbits = 60
PR.<x> = PolynomialRing(Zmod(n))
f = x + p
x0 = f.small_roots(X=2^kbits, beta=0.4)[0]
print "x: %s" %hex(int(x0))
p = p+x0
print "p: ", hex(int(p))
assert n % p == 0
q = n/int(p)
print "q: ", hex(int(q))
```

其中kbit是未知的p的低位位数  
x0为求出来的p低位

15.Partial Key Exposure Attack(给私钥d的低位)
---------------------------------------

### 场景介绍

```python
('n=', '0x56a8f8cbc72ff68e67c72718bd16d7e98150aea08780f6c4f532d20ca3c92a0fb07c959e008cbcbeac744854bc4203eb9b2996e9cf630133bc38952a2c17c27dL')
('d&amp;((1<<256)-1)=', '0x594b6c9631c4987f588399f22466b51fc48ed449b8aae0309b5736ef0b741893')
('e=', '0x3')
('c=', '0xca2841cbc52c8307e0f2c48f8b14bc0846ece4111453362e6aee4b81f44f2a14df1c58836d4937f3b868148140ee36e9a7e910dd84c2dc869ead47711412038L')
```

题目给出一组公钥n,e以及加密后的密文  
给私钥d的低位

### 攻击脚本

记N=pq为n比特RSA模数,e和d分别为加解密指数,ν为p和q低位相同的比特数,即p≡qmod2ν且p≠qmod2v+1.  
1998年,Boneh、Durfee和Frankel首先提出对RSA的部分密钥泄露攻击:当ν=1,e较小且d的低n/4比特已知时,存在关于n的多项式时间算法分解N.  
2001年R.Steinfeld和Y.Zheng指出,当ν较大时,对RSA的部分密钥泄露攻击实际不可行.

当ν和e均较小且解密指数d的低n/4比特已知时,存在关于n和2v的多项式时间算法分解N.

```python
def partial_p(p0, kbits, n):
    PR.<x> = PolynomialRing(Zmod(n))
    nbits = n.nbits()

f = 2^kbits*x + p0
    f = f.monic()
    roots = f.small_roots(X=2^(nbits//2-kbits), beta=0.3)  # find root < 2^(nbits//2-kbits) with factor >= n^0.3
    if roots:
        x0 = roots[0]
        p = gcd(2^kbits*x0 + p0, n)
        return ZZ(p)

def find_p(d0, kbits, e, n):
    X = var('X')

for k in xrange(1, e+1):
        results = solve_mod([e*d0*X - k*X*(n-X+1) + k*n == X], 2^kbits)
        for x in results:
            p0 = ZZ(x[0])
            p = partial_p(p0, kbits, n)
            if p:
                return p

if __name__ == '__main__':
    n =0x56a8f8cbc72ff68e67c72718bd16d7e98150aea08780f6c4f532d20ca3c92a0fb07c959e008cbcbeac744854bc4203eb9b2996e9cf630133bc38952a2c17c27d 
    e = 0x3
    d = 0x594b6c9631c4987f588399f22466b51fc48ed449b8aae0309b5736ef0b741893
    beta = 0.5
    epsilon = beta^2/7

nbits = n.nbits()
    kbits = 255
    d0 = d &amp; (2^kbits-1)
    print "lower %d bits (of %d bits) is given" % (kbits, nbits)

p = find_p(d0, kbits, e, n)
    print "found p: %d" % p
    q = n//p
    print hex(d)
    print hex(inverse_mod(e, (p-1)*(q-1)))
```

kbits是私钥d泄露的位数255

Padding Attack
--------------

### 场景介绍

```python
('n=', '0xb33aebb1834845f959e05da639776d08a344abf098080dc5de04f4cbf4a1001dL')
('e=', '0x3')
('c1=pow(hex_flag,e,n)', '0x3aa5058306947ff46b0107b062d75cf9e497cdb1f120d02eaeca30f76492c550L')
('c2=pow(hex_flag+1,e,n)', '0x6a645739f25380a5e5b263ff5e5b4b9324381f6408a11fdaab0488209145fb3eL')
```

原理参考  
<https://www.anquanke.com/post/id/158944>

意思很简单  
1.pow(mm, e) != pow(mm, e, n)  
2.利用rsa加密m+padding  
值得注意的是，e=3，padding可控  
那么我们拥有的条件只有  
n,e,c,padding  
所以这里的攻击肯定是要从可控的padding入手了

### 攻击脚本

```python
import gmpy
def getM2(a,b,c1,c2,n,e):
    a3 = pow(a,e,n)
    b3 = pow(b,e,n)
    first = c1-a3*c2+2*b3
    first = first % n
    second = e*b*(a3*c2-b3)
    second = second % n
    third = second*gmpy.invert(first,n)
    third = third % n
    fourth = (third+b)*gmpy.invert(a,n)
    return fourth % n
e=0x3
a=1
b=-1
c1=0x3aa5058306947ff46b0107b062d75cf9e497cdb1f120d02eaeca30f76492c550
c2=0x6a645739f25380a5e5b263ff5e5b4b9324381f6408a11fdaab0488209145fb3e
padding2=1
n=0xb33aebb1834845f959e05da639776d08a344abf098080dc5de04f4cbf4a1001d
m = getM2(a,b,c1,c2,n,e)-padding2
print hex(m)
```

通过上面介绍的那篇文章的推导过程我们可以知道  
a等于1  
b=padding1-padding2  
这边我们的padding1是第一个加密的明文与明文的差，本题是0  
padding2是第二个加密的明文与明文的差，本题是1  
所以b是-1  
我们这边是用的那篇文章的Related Message Attack

17.RSA LSB Oracle Attack
------------------------

### 场景介绍

```php
参考博客https://www.sohu.com/a/243246344_472906
适用情况：可以选择密文并泄露最低位。
在一次RSA加密中，明文为m，模数为n，加密指数为e，密文为c。
我们可以构造出c'=((2^e)*c)%n=((2^e)*(m^e))%n=((2*m)^e)%n， 因为m的两倍可能大于n，所以经过解密得到的明文是 m'=(2*m)%n 。
我们还能够知道 m' 的最低位lsb 是1还是0。
因为n是奇数，而2*m是偶数，所以如果lsb 是0，说明(2*m)%n 是偶数，没有超过n，即m<n/2.0，反之则m>n/2.0 。
举个例子就能明白2%3=2 是偶数，而4%3=1 是奇数。
以此类推，构造密文c"=(4^e)*c)%n 使其解密后为m"=(4*m)%n ，判断m" 的奇偶性可以知道m 和 n/4 的大小关系。
所以我们就有了一个二分算法，可以在对数时间内将m的范围逼近到一个足够狭窄的空间。
```

### 攻击脚本

```python
def brute_flag(encrypted_flag, n, e):

flag_count = n_count = 1
    flag_lower_bound = 0
    flag_upper_bound = n
    ciphertext = encrypted_flag
    mult = 1
    while flag_upper_bound > flag_lower_bound + 1:
        sh.recvuntil("input your option:")
        sh.sendline("D")
        ciphertext = (ciphertext * pow(2, e, n)) % n
        flag_count *= 2
        n_count = n_count * 2 - 1

print("bit = %d" % mult)
        mult += 1

sh.recvuntil("Your encrypted message:")
        sh.sendline(str(ciphertext))

data=sh.recvline()[:-1]
        if(data=='The plain of your decrypted message is even!'):
            flag_upper_bound = n * n_count / flag_count
        else:
            flag_lower_bound = n * n_count / flag_count
            n_count += 1
    return flag_upper_bound
```

18.n,e,m1,m2
------------

方法1：

题目：

```python
import hashlib
import sympy
from Crypto.Util.number import *
flag = 'GWHT{******}'
secret = '******'
assert(len(flag) == 38)
half = len(flag) / 2
flag1 = flag[:half]
flag2 = flag[half:]
secret_num = getPrime(1024) * bytes_to_long(secret)
p = sympy.nextprime(secret_num)
q = sympy.nextprime(p)
N = p * q
e = 0x10001
F1 = bytes_to_long(flag1)
F2 = bytes_to_long(flag2)
c1 = F1 + F2
c2 = pow(F1, 3) + pow(F2, 3)
assert(c2 < N)
m1 = pow(c1, e, N)
m2 = pow(c2, e, N)
output = open('secret', 'w')
output.write('N=' + str(N) + '\n')
output.write('m1=' + str(m1) + '\n')
output.write('m2=' + str(m2) + '\n')
output.close()
N=636585149594574746909030160182690866222909256464847291783000651837227921337237899651287943597773270944384034858925295744880727101606841413640006527614873110651410155893776548737823152943797884729130149758279127430044739254000426610922834573094957082589539445610828279428814524313491262061930512829074466232633130599104490893572093943832740301809630847541592548921200288222432789208650949937638303429456468889100192613859073752923812454212239908948930178355331390933536771065791817643978763045030833712326162883810638120029378337092938662174119747687899484603628344079493556601422498405360731958162719296160584042671057160241284852522913676264596201906163
m1=90009974341452243216986938028371257528604943208941176518717463554774967878152694586469377765296113165659498726012712288670458884373971419842750929287658640266219686646956929872115782173093979742958745121671928568709468526098715927189829600497283118051641107305128852697032053368115181216069626606165503465125725204875578701237789292966211824002761481815276666236869005129138862782476859103086726091860497614883282949955023222414333243193268564781621699870412557822404381213804026685831221430728290755597819259339616650158674713248841654338515199405532003173732520457813901170264713085107077001478083341339002069870585378257051150217511755761491021553239
m2=487443985757405173426628188375657117604235507936967522993257972108872283698305238454465723214226871414276788912058186197039821242912736742824080627680971802511206914394672159240206910735850651999316100014691067295708138639363203596244693995562780286637116394738250774129759021080197323724805414668042318806010652814405078769738548913675466181551005527065309515364950610137206393257148357659666687091662749848560225453826362271704292692847596339533229088038820532086109421158575841077601268713175097874083536249006018948789413238783922845633494023608865256071962856581229890043896939025613600564283391329331452199062858930374565991634191495137939574539546
```

yafu分解出pq，可解方程

```python
import gmpy2
p=797862863902421984951231350430312260517773269684958456342860983236184129602390919026048496119757187702076499551310794177917920137646835888862706126924088411570997141257159563952725882214181185531209186972351469946269508511312863779123205322378452194261217016552527754513215520329499967108196968833163329724620251096080377748737
q=797862863902421984951231350430312260517773269684958456342860983236184129602390919026048496119757187702076499551310794177917920137646835888862706126924088411570997141257159563952725882214181185531209186972351469946269508511312863779123205322378452194261217016552527754513215520329499967108196968833163329724620251096080377747699
e=0x10001
c=90009974341452243216986938028371257528604943208941176518717463554774967878152694586469377765296113165659498726012712288670458884373971419842750929287658640266219686646956929872115782173093979742958745121671928568709468526098715927189829600497283118051641107305128852697032053368115181216069626606165503465125725204875578701237789292966211824002761481815276666236869005129138862782476859103086726091860497614883282949955023222414333243193268564781621699870412557822404381213804026685831221430728290755597819259339616650158674713248841654338515199405532003173732520457813901170264713085107077001478083341339002069870585378257051150217511755761491021553239
n=p*q
phin=(p-1)*(q-1)
d=gmpy2.invert(e,phin)
m=pow(c,d,n)
print m
```

接下来解方程：

```python
from z3 import *
s = Solver()
flag1 = Int('flag1')
flag2 = Int('flag2')
s.add(flag1 + flag2 == 2732509502629189160482346120094198557857912754)
s.add(pow(flag1,3)+pow(flag2,3) ==5514544075236012543362261483183657422998274674127032311399076783844902086865451355210243586349132992563718009577051164928513093068525554)
if s.check() == sat:
    print s.model()
print hex(1590956290598033029862556611630426044507841845)[2:-1].decode('hex')+hex(1141553212031156130619789508463772513350070909)[2:-1].decode('hex')  
```

方法二脚本一把梭：

```python
#python2
import gmpy2
import sympy
N=gmpy2.mpz(636585149594574746909030160182690866222909256464847291783000651837227921337237899651287943597773270944384034858925295744880727101606841413640006527614873110651410155893776548737823152943797884729130149758279127430044739254000426610922834573094957082589539445610828279428814524313491262061930512829074466232633130599104490893572093943832740301809630847541592548921200288222432789208650949937638303429456468889100192613859073752923812454212239908948930178355331390933536771065791817643978763045030833712326162883810638120029378337092938662174119747687899484603628344079493556601422498405360731958162719296160584042671057160241284852522913676264596201906163)
e = 0x10001
m1=90009974341452243216986938028371257528604943208941176518717463554774967878152694586469377765296113165659498726012712288670458884373971419842750929287658640266219686646956929872115782173093979742958745121671928568709468526098715927189829600497283118051641107305128852697032053368115181216069626606165503465125725204875578701237789292966211824002761481815276666236869005129138862782476859103086726091860497614883282949955023222414333243193268564781621699870412557822404381213804026685831221430728290755597819259339616650158674713248841654338515199405532003173732520457813901170264713085107077001478083341339002069870585378257051150217511755761491021553239
m2=487443985757405173426628188375657117604235507936967522993257972108872283698305238454465723214226871414276788912058186197039821242912736742824080627680971802511206914394672159240206910735850651999316100014691067295708138639363203596244693995562780286637116394738250774129759021080197323724805414668042318806010652814405078769738548913675466181551005527065309515364950610137206393257148357659666687091662749848560225453826362271704292692847596339533229088038820532086109421158575841077601268713175097874083536249006018948789413238783922845633494023608865256071962856581229890043896939025613600564283391329331452199062858930374565991634191495137939574539546
n2=gmpy2.iroot(N,2)[0]
p=sympy.nextprime(n2)
q=N//p
phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)
c1=pow(m1,d,N)
c2=pow(m2,d,N)

a=3*c1
b=-3*pow(c1,2)
c=pow(c1,3)-c2
delta=gmpy2.iroot(pow(b,2)-4*a*c,2)[0]
F2=(-b+delta)//(2*a)
F1=c1-F2

print(hex(F2)[2:].decode('hex')+hex(F1)[2:].decode('hex'))
```

发表于 2021-08-25 16:19:46
阅读 ( 8749 )
分类：其他

CTF-RSA总结

0 条评论